在無線數位通訊運用上,射頻微波接收機專門處理來自天線的高頻訊號,並取得有用的資訊。靈敏度(Sensitivity)是接收機一項重要的規格,定義是能讓接收機正常工作的最小接收訊號,另外與靈敏度相關的參數包括接收系統的雜訊指數(Noise Figure, NF)、位元傳輸速率(Bit Rate),以及達到某個位元錯誤率(Bit Error Rate)所需位元能量對雜訊單邊功率頻譜密度的比值(Eb/N0),後者與採用何種調變/解調技術有關。
接收系統的雜訊指數跟數位解調所需I/Q解調之前的所有零件相關,圖1是射頻微波接收機的典型例子,稱為超外插(Superheterodyne)接收機,圖中可看出與系統雜訊指數相關的包括天線看到的外界雜訊及接收機內部的雜訊指數,後者又涵蓋了三個部分,當通道(On Channel)雜訊指數、假像頻率(Image Frequency)雜訊指數,以及本地振盪器(Local Oscillator, LO)之寬頻(Wideband)雜訊指數。
 圖1 典型的射頻微波接收機的例子
圖1 典型的射頻微波接收機的例子
熱雜訊
熱雜訊(Thermal Noise)來自導體或半導體中電荷載子的隨機運動,它在數位通訊系統效能分析中占有重要因素。載子(或電子)以一定的任意移動而形成熱平衡,此移動方式與英國植物學家羅伯特布朗(Robert Brown)發現花粉粒子在水中的運動模式類似,因此也稱布朗雜訊(Brownian Noise)。由於移動是朝任意的方向且數量很大,因此根據中央極限定理(Central Limit Theorem),所產生的電壓會是一種高斯隨機程序(Gaussian Random Process)且期望值(直流電壓)為0伏特。
不僅如此,此任意移動也會產生交流的成分,在阻抗匹配的情況下,交流電壓的變異數(Variance)與熱雜訊的平均功率成正比。一般來說,通訊接收機在阻抗匹配的情況下,根據量子力學裡的普朗克黑體輻射定律(Planck's Black Body Radiation Law)和通訊系統的推導,熱雜訊的可用功率頻譜密度(Available Power Spectral Density)可以表示為公式1[1]

....................公式1
其中h=6.6254×10-34J・s為普朗克常數,T為絕對溫度,對應到接收機的等效雜訊溫度(Equivalent Noise Temperature),k=1.38×10-23J・K-1為波茲曼常數,f為頻率,單位Hz。公式1也顯示了物質在絕對零度以上,其原子能階上一定會有隨機擾動。
大部分全世界的通訊工程師都有一個默契,即假設室溫為T=290oK,如此才能有一個明確雜訊指數的定義,圖2顯示了當T=290oK時熱雜訊的雙邊功率頻譜密度。目前無線通訊的工作頻率不會超過1,000GHz,此時公式1可以簡化為,從圖2可以看出在1,000 GHz以內幾乎為常數函數,如同白光是由各種頻率的單色光混合而成,在無線通訊領域中也稱此熱雜訊為白色雜訊(White Noise)。
 圖2 熱雜訊的雙邊功率頻譜密度函數
圖2 熱雜訊的雙邊功率頻譜密度函數
像是電阻或有損的傳輸線(Lossy Transmission Line)等這一類被動元件,在絕對溫度0oK以上就會產生熱雜訊,大氣衰減(Atmospheric Attenuation)及星際背景輻射(Interstellar Background Radiation)也會產生類似的熱雜訊。其他的雜訊源像散射雜訊(Shot Noise)、閃爍雜訊(Flicker Noise)、電漿雜訊(Plasma Noise)及量子雜訊(Quantum Noise)等,雖然源頭與熱雜訊不同,但在通訊系統的中頻(Intermediate Frequency, IF)輸出表現出來也會有類似的結果,因此皆可等效成接收機輸入端的熱雜訊[2]。舉例來說,固態的半導體元件內散射雜訊(見圖3),在單位時間內類似脈衝(Impulse)出現的機率遵循泊松分布(Poisson Distribution),其功率頻譜密度依舊是常數,因此也可以視為白色雜訊,當它在IF濾波輸出時會呈現類似圖4的結果。
 圖3 散射雜訊的時間波形
圖3 散射雜訊的時間波形
 圖4 一個理想矩形帶通白色雜訊的樣本函數
圖4 一個理想矩形帶通白色雜訊的樣本函數
熱雜訊的等效電路
圖5(a)顯示一個溫度為ToK的電阻R,假設關心的有限頻寬為B,其產生的電壓如圖5(b)所示,電壓平均值為0,其均方根電壓可表示如公式2
 圖5 (a)電阻產生雜訊電壓示意圖 (b)雜訊電壓的時間波形
圖5 (a)電阻產生雜訊電壓示意圖 (b)雜訊電壓的時間波形

....................公式2
公式2也稱為瑞雷-金斯近似(Rayleigh-Jeans Approximation)。上述的電阻利用戴維靈等效(Thevenin Equivalent)成一個戴維靈電壓和一個無雜訊的戴維靈電阻,在阻抗匹配的情況下,負載所能獲得的最大功率,也稱為可用雜訊功率 (Available Noise Power),可以計算如公式3,
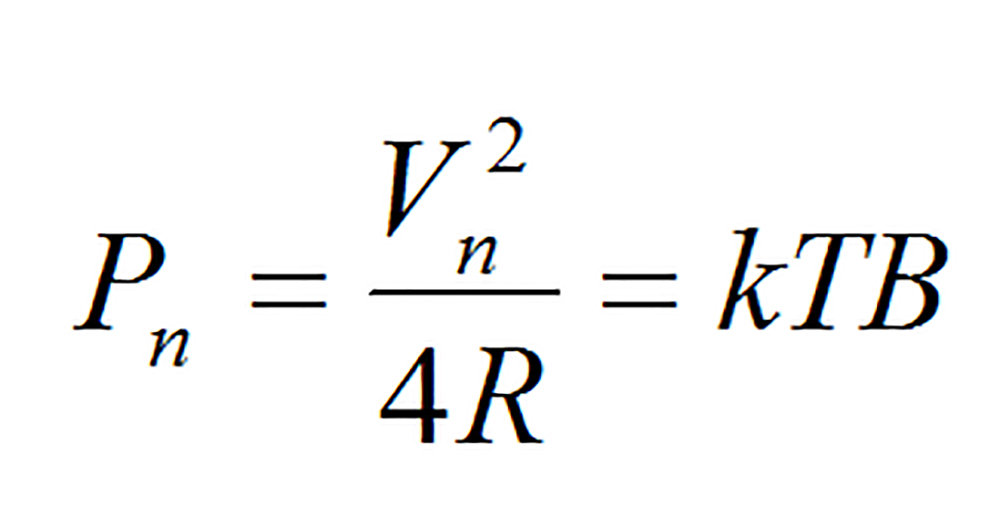
....................公式3
注意到可用雜訊功率與頻寬及溫度成正比,而與電阻大小無關。
 圖6 散射雜訊的時間波形
圖6 散射雜訊的時間波形
雜訊指數與雜訊溫度
雜訊指數(本文採用符號NF)描述一個元件所貢獻的雜訊功率,等同說法包括雜訊係數(Noise Factor,本文採用符號F)與等效雜訊溫度(Equivalent Noise Temperature, T)。以放大器為例,除了把輸入的訊號或雜訊放大,放大器內部也產生了一定量的雜訊,因此降低了輸出的訊號雜音比(Signal to Noise Ratio, S/N)。從放大器來說明雜訊係數的定義(見圖6),其中Wi(f)=kT0為進入放大器的單邊帶雜訊功率頻譜密度,W0(f)是放大器的輸出功率頻譜密度,G(f)是放大器的增益,後兩者通常是頻率的函數,雜訊係數的計算如公式4,所以雜訊係數也是頻率的函數。如果放大器內部沒有產生雜訊,則F(f)=1。

....................公式4
如果在有限頻寬為B之內,放大器的增益G(f)是常數G,公式4能改寫為公式5

....................公式5
其中Ni及No分別表示輸入及輸出的雜訊功率(在本文中勿與Eb/N0的N0搞混,No是指單邊的雜訊功率頻譜密度),假設進入放大器除了熱雜訊還有訊號,利用G=So/Si,公式5可以改寫為公式6

....................公式6
其中Si/Ni及So/No分別表示輸入及輸出的訊號雜音功率比值。
再來定義雜訊指數,一般教科書定義的雜訊指數即是將雜訊係數改用dB表示,形式如公式7,

....................公式7
最後定義等效雜訊溫度,考慮一個任意的白色雜訊源,如天線收到來自外界的熱雜訊、主動元件或被動元件產生的熱雜訊,它們都可以被看成具有等效雜訊溫度的電阻R,來取代雜訊源,重新改寫公式3可以得到等效雜訊溫度定義如公式8,

....................公式8
如果考慮增益為G的放大器,想像其輸入的雜訊功率Ni=0,放大器內部輸出的雜訊功率是No,則放大器的等效雜訊溫度為公式9。

....................公式9
再回到公式5並參考圖7,當輸入的雜訊功率Ni=kT0B,輸出的雜訊功率可以拆成兩部分,其中kT0BG是輸入的雜訊經放大器放大的結果,kT0BG(F-1)則是放大器內部自己產生的雜訊,利用公式9可以得到等效雜訊溫度與雜訊係數的關係如公式10,
 圖7 放大器內部輸出的雜訊功率示意圖
圖7 放大器內部輸出的雜訊功率示意圖

....................公式10
在此補充說明,假設兩組雜訊其電壓分別是v1(t)及v2(t),它們是兩組高斯隨機程序(Random Processes),另有一個電壓訊號是它們的和v(t)=v1(t)+v2(t),如果兩組雜訊之平均功率分別是P1、P2,v(t)的功率P需要看他們的相關係數(Correlation Coefficient) ρ(-1≤ρ≤1)才能做決定。如果ρ>0,P>P1+P2,如果ρ<0,P2mW,左圖是ρ=-0.6的情況,P<2mW。
由於進入放大器的雜訊與放大器內部產生的雜訊可以看成兩個零期望值(Zero Mean)且不相關的(Uncorrelated)高斯隨機程序,根據隨機程序的理論推導,相關係數ρ=0,所以放大器輸出的雜訊功率可以拆成兩部分,即No=kT0BG+kT0BG(F-1),分別對應到兩個不同部分的隨機程序。做個結論:兩個不相關的高斯雜訊電壓相加,其功率等於個別的功率相加。
 圖8 ρ=0的聯合機率密度函數之3-D繪圖及等高線圖
圖8 ρ=0的聯合機率密度函數之3-D繪圖及等高線圖
 圖9 ρ=0.9及ρ=-0.6的聯合機率密度函數之等高線圖
圖9 ρ=0.9及ρ=-0.6的聯合機率密度函數之等高線圖
串接元件的雜訊指數
接著仍以放大器為例,介紹兩個元件串接之後的雜訊指數。如圖10所示,假設兩個放大器都是50Ω的系統,沒有阻抗不匹配的(Mismatched)問題。
 圖10 兩個放大器串接之後的雜訊指數推導示意圖
圖10 兩個放大器串接之後的雜訊指數推導示意圖
假設兩級的參數分別是G1、F1及G2、F2,如果我們把它看成一個等效的放大器,則增益G=G1G2,雜訊指數則可推導如公式11,

....................公式11
利用公式11最後等式的兩邊同時除以kT0BG可以得到公式12,

....................公式12
依此類推,就可得到整體接收機一般式如下公式13,

....................公式13
公式13也稱作福里斯公式(Friis Formula),它有兩個含意,其一是相加的每一項代表等效到接收機最前端的雜訊量(正比於功率),其二是因為每一項兩個之間是不相關的,所以功率可以直接相加。
從公式13右邊第一項可以看到,第一級的雜訊指數對系統雜訊指數的影響很大,因此接收機進來的第一級放大器通常稱作低雜訊放大器(Low Noise Amplifier, LNA),從公式13右邊第二項之後能看到,第一級的增益對系統雜訊的抑制很重要,也就是說,LNA之後的雜訊功率影響都因為除以G1而降低了,因此得到一個結論「G1越大越好」?
然而,俗話說有一好就沒二好,太大的G1會造成接收系統的IP3降低,也因此降低了接收動態範圍(Dynamic Range);太大的G1會造成接收系統抵擋頻帶外干擾的能力降低,在接收機做阻塞(Blocking)測試時就不容易通過,因此還是得做一些折衷的判斷(Trade-off)。
將公式13做一些代數整理,可以得到串接雜訊溫度的一般式如下列公式14,

....................公式14
記得這些公式都是假設兩級之間是匹配的,對不匹配的串接有興趣的讀者可以參考教科書[2]。
有損被動元件的雜訊指數
射頻通訊系統中會有一些有損的(Lossy)元件,像衰減器(Attenuator),有損的傳輸線(Transmission Line),有置入損失(Insertion Loss)的帶通濾波器等,假設元件處在T=290oK的環境下,功率損失係數為L(L=1/G>1),由於這些元件只能衰減進入的調變訊號,無法衰減T=290oK的熱雜訊,利用公式6代入G=So/Si及No=Ni可得到公式15,

....................公式15
也就是說功率損失係數就等於是雜訊係數,例如帶通濾波器置入損失1dB,則其雜訊指數也是1dB。公式15改寫成等效雜訊溫度如下列公式16,
Te=(F-1)T0=(L-1)T0 ............公式16
如果元件不是處在T=290oK的環境下,式子會稍微複雜些,這時公式15會修正成F=1+(L-1)T/T0,其中T是環境溫度,有興趣可參考教科書[2],由於通訊環境溫度不會偏離T=290oK太多,因此記得簡單公式15已經足夠了。
例如T=27oC=300oK,F=2,修正後F'=1+(2-1)×300/290=2.03,以dB來看,原來NF=3dB,修正後NF'=3.08dB,這種誤差是可以忽略的。
被動混波器(Mixer)通常是由二極體組成,其雜訊指數一般的做法就是置入損失加上0.5~1dB,以Mini-Circuits的RMS-2為例,它是一顆雙平衡(Double-balanced)結構的混波器,其置入損失為7.5dB,因此一般的說法就是雜訊指數8dB。
天線雜訊溫度
接收系統的雜訊指數包含了兩個部分,一個是天線看到的雜訊所得到的,通常是用天線雜訊溫度表示,另一個則是接收機的雜訊指數,在此先討論天線雜訊的溫度。
天線雜訊的來源包括天線從外界環境所收集到的雜訊,以及天線因為內部損失所形成的熱雜訊,在天線與後級匹配的情況下,可以用公式17表示,
Ta=ηTb+(1-η)Tp ...................公式17
其中Ta稱為天線雜訊溫度(Antenna Noise Temperature),TP是天線的實際溫度(Physical Temperature),η是天線效率(Efficiency),Tb是天線等效的亮度溫度(Brightness Temperature),Tb越大表示天線場型往外收集的雜訊越多。理想的天線效率η=1,此時Ta=Tb。
為了說明亮度溫度,在此把天線從外界環境所收集到的雜訊,假想成電阻R被放在某個環境溫度下的結果,此等效的溫度稱為背景雜訊溫度(Background Noise Temperature) TB。例如,參考圖11,其中θ稱為高度角(Elevation Angle),此天線場型垂直朝向天空(θ=0o),或者說仰角90o,主波束(Main Beam)夠窄使得其看到的雜訊溫度是均一的(Uniform),將收集到的雜訊功率對頻率與角度做歸一化(Normalized)處理,得到TB(θ=0o,𝜙=0o),依此類推,改變各種角度就可以得到TB(θ,𝜙)函數。再回到真實的天線,以此天線的功率場型函數(Power Pattern Function) D(θ,𝜙)為權重,兩者做加權平均即可得到天線等效的亮度溫度Tb。
 圖11 主波束夠窄的天線場型示意圖
圖11 主波束夠窄的天線場型示意圖
舉個例子,如果在較低的微波段,朝天頂(Toward Zenith)的背景雜訊溫度約為3~5K,隨著高度角θ增加,或者說仰角減少,背景雜訊溫度會升高,一直到向地平線(Toward Horizon)約為50~100K,當θ≤-10o,背景雜訊溫度約為290~300K。宇宙從大爆炸(Big Bang)的極高溫經宇宙膨脹至今,殘留的宇宙背景輻射(Cosmic Background Radiation)約為2.7K,這大概是TB的極限值,不能再低了。
背景雜訊溫度與頻率有關,也與天線指向的地方出現的天體有關,例如指向銀河系,雜訊溫度又會明顯增加,有興趣的讀者可以參考教科書[2]或其他與天線相關的書籍。
天線等效的亮度溫度Tb是背景雜訊溫度經由功率場型函數加權的結果,通常兩個山頭頂端的點對點微波轉播系統約為150K。有高度的基地台天線指向地球表面則約為290~300K。一般在地球表面做通訊,以基地台採用半波偶極天線或以手機通訊為例,我們可以直接把天線等效的亮度溫度設定為Tb=290oK。
接收天線輸出的熱雜訊在時間上的表現像圖5(b),進入接收機後從中頻(IF)輸出,其表現則類似圖12,圖中顯示了四個樣本函數。再次強調,不管是甚麼雜訊,經IF的通道濾波器濾波後其統計特性都差不多了。
 圖12 熱雜訊經IF的通道濾波後之樣本函數圖
圖12 熱雜訊經IF的通道濾波後之樣本函數圖
接收機的雜訊指數
接收機的雜訊指數可以分成三個部分來討論,包括當通道(On Channel)雜訊指數、假像頻率(Image Frequency)雜訊指數,以及本地振盪器(Local Oscillator, LO)之寬頻(Wideband)雜訊指數。由於這三種雜訊是不相關的且與對應的雜訊係數與功率成正比,因此它們的雜訊係數可以直接相加如公式18[3]:
FR=FIN+F'IN+F''IN ....................公式18
其中FIN是等效到接收機輸入端的當通道雜訊係數,F'IN是等效到接收機輸入端的假像頻率雜訊係數,F''IN是等效到接收機輸入端的本地振盪器之寬頻雜訊係數。
當通道雜訊係數由每一級個別的增益 Gn與雜訊指數Fn來決定,類似公式13,參考圖13重寫如公式19,其中定義G0=1。

....................公式19
假像雜訊是出現在混波器之前位在假像頻率處的雜訊,如圖14所示中央的X的部分,其來源可以是外來的或是前級放大器內部產生的。假像雜訊經由混波器降頻後會出現在中頻(Intermediate Frequency, IF)處,通常會與當通道訊號有相同的轉換損失(Conversion Loss)。假像雜訊係數一般可以表示成公式20,其中Gn'為假像頻率增益,Fn'為假像頻率雜訊係數。公式20通常只要考慮到混波器之前即可,即公式20中的N1,因為當它進入中頻後,與當通道雜訊會有相同的經歷過程。
 圖13 接收系統簡易方塊圖
圖13 接收系統簡易方塊圖
 圖14 假像雜訊示意圖
圖14 假像雜訊示意圖

....................公式20
需特別說明的是如果接收鏈路有出現假像頻率排斥濾波器(Image Reject Filter),如圖1顯示,可以設定其單一的假像頻率雜訊係數為1,在此情況下整體的假像頻率雜訊係數通常可以忽略不計。另一個極端情況下,混波器之前當通道與假像頻率的個別增益/衰減及雜訊係數都一樣,此時兩者的整體雜訊係數會相同。
本地振盪器之寬頻雜訊會出現在混波器的LO端,這些寬頻雜訊進入混波器後有一部分也會出現在中頻處,如圖15中所看到的6個X的部分,因為它們與nfLO相隔fIF的距離。
 圖15 寬頻雜訊示意圖
圖15 寬頻雜訊示意圖
由於LO的緩衝放大級(Buffer Amplifier)的關係,寬頻雜訊的功率頻譜密度會遠高於熱雜訊。當然它們也會比當通道的轉移損失大很多,寬頻雜訊到達中頻的損失稱作MNB(Mixer Noise Balance),其值必須額外的做量測才能獲得,以雙平衡式混波器為例,其MNB大約落在20~30dB之間,若採用單端混波器(Single-ended Mixer),則完全沒有排拒寬頻雜訊的能力,此時一定要考慮在LO端放置注入濾波器(Injection Filter),圖16為放置注入濾波器的示意圖。
 圖16 放置注入濾波器示意圖
圖16 放置注入濾波器示意圖
寬頻雜訊係數一般可以表示成公式21,其中PLO(dBm)是LO端進入混波器的功率,WS(dBc/Hz)是相對於LO端功率的寬頻雜訊功率頻譜密度,MS(dB)是MNB,M是考量的旁波帶(sideband)個數,以圖15為例,M=6。如果LO端有放置注入濾波器(Injection Filter),則其對旁波帶的損失以LS(dB)表示,若無則LS=0dB。公式21的分母要考慮到混波器為止,即N1+1。另外分母的1000是為了配合分子的單位是mW。

....................公式21
參考書籍[3]舉了一個例子,計算結果其中FIN=8.63,F'IN=0.63,F''IN=5.62,相加得到FR=14.88。從例子中得到第一個結論,由於例子[3]中有假像頻率排斥濾波器,所以假像頻率雜訊係數可以忽略。
一般的射頻系統工程師通常只考慮FIN=8.63這一項,事實上大部分的接收系統確實可以只考慮當通道雜訊係數,這是因為混波器之前如果有足夠的增益,就是公式21分母裡的夠大,則寬頻雜訊係數就可以忽略。
在參考書[3]的例子裡,混波器之前只有兩個濾波器夾了一個放大器,增益是-2.5 dB+12dB+(-2dB)=7.5dB,由於增益太小,因此凸顯了寬頻雜訊係數的重要。典型的接收機設計,混波器之前不會有這麼小的增益,因此忽略寬頻雜訊是可行的。
接收系統前端的等效熱雜訊底層
討論至此有一個大哉問,接收系統前端的等效熱雜訊底層(Noise Floor)到底是多少?由公式17得知,天線收到的等效熱雜訊溫度為Ta=ηTb+(1-η)Tp,由公式18也知道接收機在中頻以前的射頻電路貢獻的輸入端等效雜訊係數為FR=FIN+F'IN+F''IN,由於兩者是不相關的,因此接收系統前端的等效熱雜訊可以表示為兩者相加,即接收系統整體雜訊溫度TS=Ta+(FR-1)T0,等效熱雜訊底層如公式22a,
kTS=kTa+k(FR-1)T0 .............公式22a
通訊工程師習慣在描述接收機時使用雜訊指數,因此改寫如公式22b
kTS=kTa+k(10NFR/10-1)T0 ...........公式22b
針對不同的天線雜訊溫度,我們把公式22b畫成圖17,其中縱軸採用dBm/MHz的單位。先觀察Ta=T0=290K的直線,這也是一般行動通訊採用的直線,如果接收機的雜訊係數NFR=0dB,雜訊底層為-114dBm/MHz,NFR每增加1dB,雜訊底層就增加1dB,例如NFR=10dB,雜訊底層為-104dBm/MHz。
 圖17 不同天線溫度與接收機雜訊指數和接收系統雜訊底層的關係圖
圖17 不同天線溫度與接收機雜訊指數和接收系統雜訊底層的關係圖
另外有一個極端的例子,即Ta=2.7K的曲線,這時接收機的雜訊係數NFR就變得相對重要,以宇宙微波背景輻射量測為例,參考圖18,其中LNA是放置在4K的液態氦內,有極低的雜訊指數,透過適當的校正,可以反推宇宙溫度為2.7度K。
 圖18 宇宙微波背景輻射量測的方塊圖
圖18 宇宙微波背景輻射量測的方塊圖
雜訊指數的量測
繼續以放大器為例,介紹低雜訊放大器雜訊指數量測原理。一種常用的技巧稱為Y係數法(Y-factor Method),此方法需要兩個雜訊源,通常一個是置於室溫下的50Ω負載(Load),也叫做冷雜訊源,另一個是經準確校正好的熱雜訊源,其過量雜訊比值(Excess Noise Ratio, ENR)已知。
參考圖19,對應的ENR可以用累增崩潰二極體(Avalanche Diode)所組成電路,例如HP 346B,此雜訊源在接上+28V時,是個等效熱雜訊源,量得功率為N1,此雜訊源不接上電源時,是個等效冷雜訊源,量得功率為N2,Y係數法的 Y=N1/N2,代入下式可得:
 圖19 等效雜訊溫度量測圖
圖19 等效雜訊溫度量測圖

....................公式23
上面提到的頻譜分析儀(SA)如果是傳統式,在量測雜訊功率時須做一些修正,不同廠牌會有不同的修正因數(Correction Factor)。如果本身就有雜訊指數量測功能,儀器內部本身就會做好修正的工作。為什麼要修正?原因有3個,一是SA利用峰值檢測(Peak Detector)量振幅,但是雜訊需要量測的是均方根值,二是SA的中頻解析頻寬(RBW)小於雜訊的等效頻寬(Equivalent Bandwidth),三是SA的螢幕顯示是對數的(Logarithmic)運算結果,較低的讀值(Reading)通常會被放大。
在此以5.7GHz低雜訊放大器做為量測實例,使用購買的ENR套件來結合SA(HP 8590)做量測,雜訊指數的計算是頻譜分析儀內部完成的,圖20為所測得的5.7GHz低雜訊放大器雜訊指數,在5.725~5.825GHz頻率範圍內,雜訊指數都低於1.6dB[4]。
 圖20 5.7GHz低雜訊放大器雜訊指數量測圖
圖20 5.7GHz低雜訊放大器雜訊指數量測圖
如果單獨量測混波器的雜訊指數,將會面臨一個難題,同樣以Mini-Circuits的RMS-2雙平衡混波器為例,過去曾經請儀器公司的工程人員在實驗室做了兩次量測,尚未測試之前答覆都能達到要求,但測試後都以失敗結束,原因就是做冷雜訊源量測時,混波器會有n次諧波出現,會嚴重影響N2的功率量測,另一個影響的因素是LO的寬頻雜訊造成的輸出可能會蓋過N2的雜訊量。
我們以Builder模擬來說明,圖21左邊是冷雜訊-114dBm/MHz,LO功率-7dBm,頻率500MHz,進入混波器得到圖21右圖,由圖21右圖可以看見明顯的5根諧波,功率遠大於N2。
 圖21 雙平衡混波器雜訊量測圖
圖21 雙平衡混波器雜訊量測圖
另一個問題是被動混波器衰減7.5B,但是輸出雜訊卻明顯增加,這是LO的寬頻雜訊造成的結果。這兩個問題需要解決才能量測混波器的雜訊指數。通常變通的方式就是直接講出來,比衰減多0.5~1dB就是被動混波器的雜訊指數了。
接收機靈敏度與無交互調變失真
接收機靈敏度(Sensitivity)定義為能使接收機正常工作的最小接收訊號,針對數位通訊系統,靈敏度可以計算如公式24,
S(dBm)=-144(dBm/kHz)+NFs+ 10log(Rb)+Eb/N0+Lsys ........公式24
其中NFs(dB)為接收機的雜訊指數,Rb為位元傳輸速率,單位kbps(Bit Per Second)或kHz。Eb/N0(dB)為位元能量對單邊雜訊功率頻譜密度的比值。 Lsys(dB)為系統損失,通常是各種電路不夠完美造成的,有時候也稱做實作損失(Implementation Loss),此項若不易預估則設為0dB。
接收機的雜訊指數,一般對應到圖17中Ta=T0=290K的直線,這是因為當我們做靈敏度量測時,進入接收機之前會置放固定及可調衰減器(Attenuator),從衰減器往前看,環境溫度不會偏離T=290oK太多,因此測試環境等同於Tb=290oK的直線。
位元傳輸速率Rb直接影響靈敏度,做太空通訊時,假設無人太空船要從太陽系外圍送回探測資料,由於距離太遠,自由空間衰減非常嚴重,因此必須採用極低的位元傳輸速率(例如Rb=300bps)才能達到靈敏度的要求。
與Eb/N0要求相關則包括調變技術、解調方法及要求的位元錯誤率,假設接收端採用一致的解調,幾種常見的技術其BER與Eb/N0的關係如圖22所示。
 圖22 不同調變技術最佳解調性能的比較
圖22 不同調變技術最佳解調性能的比較
例如,假設接收系統可接受之位元錯誤率為BER=10-4,則π/4-DQPSK同調解調所需之Eb/N0=8.5dB(參考圖22),訊號傳輸速率Rs=1.536Msymbol/sec,即Rb=1536*2kbps,一個5.7GHz接收模組整體雜訊指數約4.7dB,故由靈敏度的定義可得到預估數值:S=-144+4.7+10log(3072)+8.5=-95.9dBm。
實際量測借用數位音訊廣播(Digital Audio Broadcasting, DAB)系統之Philips DAB Test Encoder及DAB Test Receiver,配合5.7GHz收發模組來測試OFDM結合π/4-DQPSK (Eureka 147, Mode I)之數位傳輸系統[4]。量測所得的靈敏度約為S=-93dBm,與預估值相差約2.9dB,推測誤差來自:(1)理論推導假設儀器與測試環境都是完美的,實際上例如雜訊指數4.7dB只包含5.7GHz降頻至DAB Test Receiver輸入端192MHz的部分;(2)OFDM的保護時間(Guard Time)浪費了約10*log(1000/1246)=-0.96dB;(3)電路不完美造成,例如相位雜訊(Phase Noise)等。
無交互調變失真動態範圍(Intermodulation-free Dynamic Range, IFDR)是另一項與接收機相關的系統規格,有些書本稱作Spurious-free Dynamic Range。IFDR定義為做雙頻測試時,假設我們要的訊號功率是Pf1,三階交互調變失真功率是P(2f1-f2),當後者等於輸出雜訊功率時,,經過整理計算後[2], 可以得到公式25a或25b,
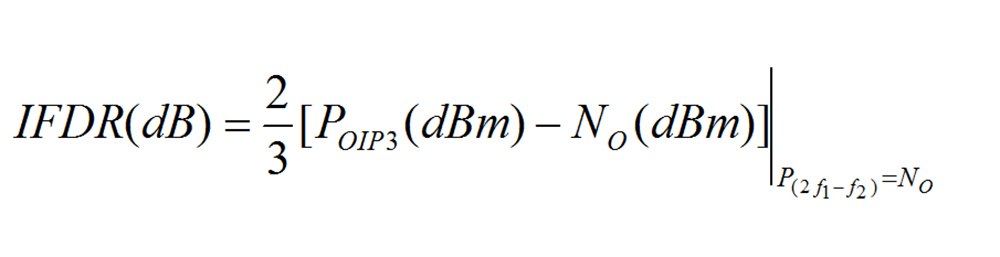
....................公式25a

....................公式25b
其中,POIP3(dBm)為接收機的輸出IP3,No(dBm)為接收機的輸出雜訊功率,兩者通常考慮到IF端。B(kHz)為等效的雜訊頻寬,通常是通道(Channel)頻寬,G(dB)為接收系統增益,NF則是本文的主題:接收系統的雜訊指數。IFDR代表接收系統的非線性與雜訊的綜合指標,它跟增益的分佈有相關性,增益分佈偏向天線端,NF會改善,但POIP3(dBm)會變差。
最後我們舉一個數字的例子,假設POIP3=36dBm,G=40dB,Ta=290oK,NF=5dB,B=1MHz,計算IFDR如下:


(本文作者為南台科技大學電子工程學系助理教授)