射頻與微波頻率合成器經常採用多個相連的鎖相迴路(Phase-Locked Loop, PLL)，這些架構提高了複雜性以換取改善相位噪聲、更小的頻率步長和更快的切換[1]。在時脈應用中，或許還可以採用多重的PLL以組合時脈功能和/或形塑相位噪聲。
例如有文章曾介紹用於小型基地台應用的無線抖動衰減器，使用芯科科技(Silicon Labs)的DSPLL雙迴路架構[2]。這種做法是一種巢套(Nested)雙迴路，而不是串接(Concatenated)式雙迴路。這種實行方式有其明確的優點和一些重要的考量。 其中一種考量是內外迴路之間必要的頻寬關係，例如當內迴路與外迴路的頻寬相差無幾，可能導致所謂的「迴路對抗」現象。第二個考慮因素是，如何分析由串接與巢套這兩種方法之間的根本架構差異所引起的相位噪聲。
本文將分為兩部分，描述把雙迴路架構運用在時脈應用中的細微差別。第一部分是在比較串接(串聯)式雙迴路PLL與巢套雙迴路PLL架構；第二部分則是用簡化的例子來進一步描述，這兩種雙迴路PLL做法的相位雜訊如何計算。
首部曲—巢套雙迴路vs.串接式雙迴路架構
基本的鎖相迴路時脈應用有兩種[3]：時脈產生器(又稱作時脈倍增器、倍頻器等)與抖動衰減器(又稱作抖動清除器)。
串接式雙迴路PLL架構
低雜訊的參考時脈是時脈產生器的輸入，頻寬通常偏寬(例如幾百kHz到MHz)。相形之下，抖動的時脈則是抖動衰減器的輸入，頻寬通常偏窄，為kHz以下的級數。
但要是時脈應用同時需要這兩種功能呢？最直接的做法就是以串聯來串接兩個PLL。
圖1呈現的是單晶片、串接式(Cascade)雙迴路架構。(請留意，串接在這層的意義跟典型的控制系統術語有所不同。在此是指兩個PLL串級或串聯起來。)
圖1 單晶片串接式雙迴路架構
在此案例中，左邊的PLL1是靠著類比的壓控晶體振盪器(VCXO)來當成窄頻段的抖動衰減器級。經過抖動衰減的時脈訊號接著輸入右邊的PLL2，以PLL2當成寬頻的時脈產生器級。壓控晶體振盪器的頻率不需要非常高，但要有良好的近端相位噪聲。這通常意謂晶體具有高Q值，這就是為什麼該元件通常位於IC外部的原因。向VCXO提供外部控制電壓訊號有其必要。而晶片上壓控振盪器(VCO)的頻率需要夠高，以便除頻後的時脈能夠產生必要的輸出時脈頻率。在高偏移頻率下它還應該具有低相位雜訊。
這個例子是描述全類比，有數個外部濾波器元件和敏感線路。然而為什麼串接式雙迴路架構無法以數位方式且在晶片上濾波來實現，並沒有先天上的理由。在上述的例子中，由於PLL是串聯而獨立，總輸出相位雜訊便能依照在[3]中所描述相位雜訊處理要素的串接來計算。
巢套雙迴路PLL架構
圖2呈現的是巢套雙迴路架構。在典型的控制系統術語中，這將被視為串接式控制系統的變體。為了清楚起見，在此會使用巢套這個詞，將其視作相當於俄羅斯娃娃的PLL。
圖2 巢套雙迴路架構
在此案例中，內迴路(Inner Loop, IL)鎖相迴路被用作外迴路(Outer Loop, OL)的「壓控振盪器」，要不然就是數位控制振盪器(DCO)。這是這兩種做法的根本差異，它將決定如何計算總相位雜訊。
這是如何運作？
1. OL數位迴路濾波器的輸出調變IL的返迴路徑。
2. IL壓控振盪器的輸出實際上就是圖2中的fOUT。在實務上，這個輸出頻率會進一步劃分，以產生必要的輸出時脈。
這種做法的優點是什麼？在這對例子中，本文把調諧振盪器的數目從兩個(壓控晶體振盪器和壓控振盪器)縮減成一個(晶體振盪器和壓控振盪器)。這消除了一個迴路濾波器(不管是內部還是外部)和敏感的電壓控制線的需求，否則就必須從外部來走線。元件的減少使解決方案更加簡潔，進而減少整體PCB布線。
是否能以壓控晶體振盪器來實現巢套雙迴路？原則上可以，沒有原因顯示為什麼不能實現同時使用外部壓控晶體振盪器的巢套雙迴路架構。如果特定的壓控晶體振盪器有較好的相位雜訊效能，也許在更高的頻率(更新速率)下，這樣的做法或許甚至是更有意義。不過，就會喪失前面所討論到的具體優點，包括減少元件數量、簡化設計的複雜性，以及減少整體印刷電路板的布線等。這就是為什麼某些無線抖動衰減器如Si538x不支援外部壓控晶體振盪器。
「對抗」究竟是什麼？
在這類的巢套反饋控制迴路中，內迴路必須比外迴路要快。假如迴路的速度不相上下，那麼迴路就會彼此相爭或「對抗」(Duel)。
用PLL術語來說，內部迴路必須具有比外部迴路更寬的頻寬。如果考慮將非常慢的數位控制振盪器插入原本快速的鎖相迴路，對照將一個非常快速的DCO插入原本偏慢的鎖相迴路，直觀上的差異，前例會顯著影響到鎖相迴路，甚至由於插入的額外延遲可能具有穩定性或鎖定問題。相較之下，後例不會受到明顯影響。這表示，內迴路必須是較快(頻段較寬)的時脈倍頻器，外迴路必須是較慢(頻段較窄)的抖動衰減器。此外，它還顯示，在啟動和鎖定過程中，希望內迴路PLL在外迴路之前穩定並鎖定。
以另一種方式思考，別忘了對於迴路中的任何來源所造成的相位雜訊，PLL的功能便是作為低通濾波器，例外則是當成壓控振盪器相位雜訊的高通濾波器時。外迴路PLL如果要調變內迴路的返回路徑而不衰減，訊號就必須大幅落在內迴路的頻寬內。
順帶一提，如果想從某個量估算另一個量，例如從PLL頻寬估算出頻率步進上升時間，就可利用以下關係式：
Tr[10%-90%]*BW[3dB]≈0.35
例如參見Howard Johnson在文章PLL Response Time[5]中的討論。根據此文，時間頻寬乘積從0.35到0.38不等，這取決於PLL的表現較接近單極還是雙極響應。
內迴路必須多快或多少頻寬？在機械工程和程序控制系統中，巢套迴路速度的差異可能相對較小。機械內迴路或許會比機械外迴路要快5至10倍，可參考Danielle Collins談伺服迴路(Servo Loop)的文章[6]。然而，在時脈應用中，頻寬的差異一般則要大得多。巢套雙迴路的內迴路頻寬一般都是MHz的級數，外迴路頻寬則可能是10Hz到1kHz的級數，所以比率更接近於內迴路比外迴路要快1,000至100,000倍。
舉例來說，Si538x元件的內迴路頻寬夠寬(~1MHz)、固定且經過最佳化。由於它如此寬，因此Si538x的晶體振盪器(XO)輸入、也就是XA/XB接腳便沒有抖動衰減。因此，應該注意雜訊和干擾並不會透過這些接腳上的XO電路耦合到裝置中。這就是為什麼本文建議低相位雜訊XO要擺得盡可能靠近裝置，大幅減少PCB布線的長度。
這個想法是否可以延伸？
原則上可以。前面所引用的伺服控制迴路文章，討論了伺服馬達控制的三個巢套迴路，從內到外分別為：電流反饋、速度反饋和位置反饋。類似的是，可以「三倍巢套迴路」時脈PLL來形塑相位雜訊，以便在不同的偏移頻率下追蹤相位雜訊特性不同的選取輸入時脈。但是，Si538x元件並未使用這種作法。
二部曲—計算兩種雙迴路PLL方式的相位雜訊
本段落透過簡化的例子，詳細解釋針對串接(串聯)式雙迴路PLL和巢套雙迴路PLL這兩種雙鎖相迴路方式的相位雜訊要如何計算。
一些簡化的假設
為了強調基本觀念而不要糾結在太多的細節上，在此提出以下簡化的假設：
1. 抖動產生，即PLL固有的雜訊可以忽略不計。只關心PLL是怎麼為各自的相位雜訊來源濾波，以及它們如何影響輸出時脈的相位噪聲。
2. 不需要相位噪聲的調節。假設使用的相位噪聲數據是在兩個PLL的相同載波頻率下所採集的。例如，好比有一個54MHz的晶體振盪器或壓控晶體振盪器，輸入和輸出時脈頻率都是54MHz，而且壓控振盪器的相位雜訊已縮減至54MHz。(否則便需要調節相位雜訊的數據。)
3. 透過相同的相位噪聲來源比較兩種拓撲。尤其是，假設晶體振盪器和壓控晶體振盪器的相位雜訊是相同的。普遍來說，情況並非如此，在相同的標稱頻率下，壓控晶體振盪器通常會比晶體振盪器來得有雜訊。為什麼要採用這個假設，本文後段會加以說明。
4. PLL分別作為輸入和壓控振盪器的相位雜訊的低通濾波器(LPF)或高通濾波器(HPF)。濾波器是以頻寬(BW)頻率的角頻率為範本。濾波器的裙帶斜度或陡度是20dB/dec乘以鎖相迴路級數。所以第二級的PLL會以40dB/dec的濾波器斜度為範本。
串聯式雙迴路相位雜訊的計算
回過頭檢視本文前面部分提及的圖1，其中兩個PLL彼此串聯。請注意，第一個鎖相迴路PLL1是窄頻(NB)，第二個鎖相迴路PLL2則是寬頻。為了計算相位噪聲，將從左到右來進行以下步驟。
1. 根據PLL1的頻寬來替輸入時脈的相位噪聲進行低通濾波。
2. 根據PLL1的頻寬來替壓控晶體振盪器的相位噪聲進行高通濾波。
3. 以功率意義上將它們的貢獻相加，以得出PLL1對PLL2的總相位噪聲輸入。
4. 根據PLL2的頻寬來替對PLL2的輸入進行低通濾波。
5. 根據PLL2的頻寬來替壓控振盪器的相位噪聲進行高通濾波。
6. 最後，靠功率意義把後面這兩筆作用加在一起，以得出總輸出相位噪聲。
將這些計算做成試算表，PLL假定為第二級，窄頻PLL的頻寬=100Hz，寬頻PLL的頻寬=1MHz。這些參數可在試算表中更改，但在實務上來說，窄頻PLL會是mHz到kHz的級數；寬頻PLL一般則是500kHz到2MHz，結果如圖3所示。
圖3 串聯式雙迴路相位雜訊的計算結果
巢套雙迴路相位雜訊的計算
回到第一部分所引用的圖2，在此案例中，兩個PLL相互巢套。
此時內迴路(IL)PLL是寬頻，外迴路(OL)PLL則是窄頻。為了計算相位噪聲，將透過以下步驟「由內而外」進行。
1. 根據內迴路PLL的頻寬來替晶體振盪器的相位噪聲進行低通濾波。
2. 根據內迴路PLL的頻寬來替壓控振盪器的相位噪聲進行高通濾波。
3. 靠功率意義把它們的作用加在一起，以得出總內迴路相位噪聲。別忘了內迴路PLL是當成外迴路PLL的「壓控振盪器」。
4. 根據外迴路PLL的頻寬來替輸入的相位噪聲進行低通濾波。
5. 根據外迴路PLL的頻寬來替總內迴路的相位噪聲進行高通濾波。
6. 靠功率意義將後面這兩筆作用加在一起，以得出總輸出相位噪聲。
這些計算也可做成試算表。如前所述，為了讓簡化的範例保持正確的對應關係，PLL假定為第二級，窄頻PLL的頻寬=100Hz，寬頻PLL的頻寬=1MHz。結果繪圖如圖4所示。
圖4 巢套雙迴路相位雜訊的計算結果
請留意這些結果圖之間的相似度，將輸出相位噪聲的繪圖套疊在一起進行比較。
串聯式與巢套雙迴路相位雜訊繪圖
輸出相位噪聲繪圖套疊在彼此上方，進行直接比較。如圖5所示，它們看起來是相同的。更有甚者，假如針對各拓撲來實驗每個PLL的頻寬，一般透過將PLL1(即外迴路PLL)和PLL2(即內迴路PLL)各自設為窄頻和寬頻，可獲得最佳的輸出相位噪聲。即使不考慮穩定性，這兩種拓撲也受益於頻寬之間的廣泛分隔。
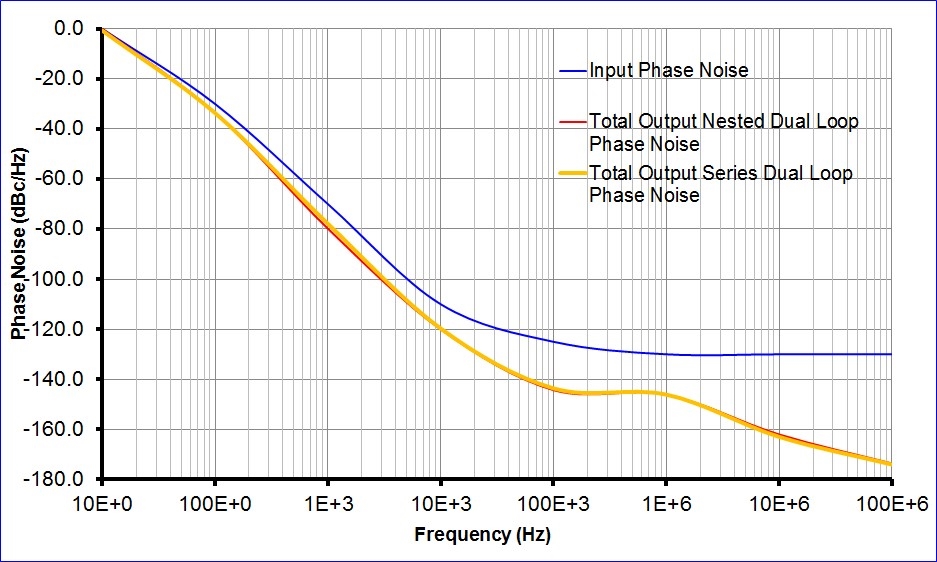圖5 串聯式與巢套雙迴路相位雜訊繪圖比較
為什麼會有拓撲等價(Topological Equivalence)？
這樣的結果不必然會預期到，所以本文把步驟再走一遍，以比較做法。
1. 總串聯式雙迴路相位雜訊可以寫成：
LPF_WB(LPF_NB(Input)+HPF_NB(VCXO))+HPF_WB(VCO)
LPF_WB*LPF_NB(Input)+LPF_WB*HPF_NB(VCXO)+HPF_WB(VCO)
使用寬頻和窄頻的標記來對照PLL1、PLL2、內迴路PLL和外迴路PLL，是為了幫助本文對兩組計算進行直接比較。LPF_WB是指將寬頻低通濾波器套用在括號中的相位噪聲上。兩個濾波器項目相乘則是指，對兩個濾波器都加以套用。
2. 類似的是，總巢套雙迴路相位噪聲可以寫成：
LPF_NB(Input)+HPF_NB(LPF_WB(XO)+HPF_WB(VCO))
LPF_NB(Input)+HPF_NB*LPF_WB(XO)+HPF_NB*HPF_WB(VCO)
3. 如果所牽涉到的頻寬相同，而且壓控晶體振盪器的相位噪聲等於晶體振盪器的相位噪聲，那上述的中間項目相等，這些可以想成是「頻通(Bandpass)」項目。
4. 此外，假設各頻寬之間有足夠的區隔，就能提出以下的概算：
LPF_WB*LPF_NB(Input)≈LPF_NB(Input)
HPF_NB*HPF_WB(VCO)≈HPF_WB(VCO)
換句話說，窄頻低通濾波器和寬頻高通濾波器主導了這些低通濾波器和高通濾波器項目的計算。這就是為什麼當其他條件相等時，這些拓撲所產生的總相位噪聲會相當。
結語
運用如本文第一部分所描述的巢套雙迴路方法時，實務上的優點包括，調諧振盪器的數目會從兩個縮減至一個，以及消除對敏感的外部電壓控制線的需求。巢套反饋控制迴路的權衡在於，內迴路必須比外迴路要快。假如迴路的速度(或頻寬)相當，那麼迴路就會彼此相爭或「對抗」。
第二部分更詳細地介紹關於串聯式和巢套雙迴路的做法，兩者的相位雜訊要如何計算。透過將頻寬廣泛區隔的簡單例子，可以看到這些做法本質上是相當的。然而，巢套雙迴路的做法也有優勢，以交替的實務施行所產生的相位雜訊，會與串聯式雙迴路的做法相當。如Si538x無線裝置便是這種寬頻IL巢套雙迴路做法的例子，可實現良好的效能，同時以較簡單的晶體振盪器取代壓控晶體振盪器。
(本文由芯科科技提供)