近幾年,手機無線定位架構獲得許多研究。無線定位技術已有許多的方法,包括訊號強度、抵達時間、抵達角度與抵達時間差等。訊號強度利用已知的訊號衰減模型獲得距離量測;抵達時間量測訊號傳輸的時間;抵達角度利用在服務基地台的天線陣列獲得角度的量測,而抵達時間差為了抵銷行動定位裝置與基地台系統之間的同步誤差效應,量測訊號傳輸的時間差。角度量測至少需要兩個基地台,不須要做時間同步;時間量測至少需要三個基地台,雖然須要同步,但精確度比較高。
無線定位技術已經有許多應用,包括緊急救援和智慧運輸系統。緊急救援需要精準地知道待援者的電話號碼與所在位置;而智慧運輸系統則是下一代的運輸系統,結合了傳統運輸系統、電子技術、控制、電腦和管理策略。智慧運輸系統利用定位技術,提高運輸系統的效率與安全度,降低交通壅塞與改善收費可靠度。
自動車輛位置技術是一種基於電腦,從中央控制決定車輛的位置。自動車輛位置技術通常是實現複雜智慧運輸系統的第一步,很多智慧運輸系統的應用都須要用到自動車輛位置技術,例如個人導航、車輛引導與公共運輸控制。
自動車輛位置技術有許多種類,包括航位推算、手持式裝置近接輸入偵測系統與無線電定位系統。航位推算在物體移動時,利用先前預估位置的方法,推算物體的速度與移動方向,得知物體的位置。而手持式裝置近接輸入偵測系統辨認車輛通過的最新路標,利用每個車輛的無線電連結,偵測現在位置。為了有高精確度的大覆蓋面積,需要許多額外的路標,這需要許多的金錢來運作與維護。以上兩種方法都要有額外的設備架設在車輛上。而無線電定位系統利用車輛間與固定場站的無線電傳輸的參數,進行車輛的定位。
偵測力會是另一個議題,影響無線定位技術的選擇方法。偵測力被定義為行動台能夠同時偵測到多少周遭的基地台、能達到的訊雜比程度。舉例來說,行動台在鄉下偵測力不佳,由於每個基地台覆蓋的範圍都十分廣大。一份論文提到,接收訊號強度大於-100分貝(dB)的機率,鄉下地區約為35%,而城市地區約為84%。缺乏能運用的基地台,會成為無線定位技術的考驗之一。
善用演算法 提升精確度
為了提升行動裝置無線定位的精確度,這裡將應用混合兩種機制的演算法:抵達時間差與抵達角度的混合。假設行動台附近有三個基地台能夠提供抵達時間的量測,與最近的服務基地台能提供抵達角度量測,利用這些資訊進而估測行動台的位置。模擬結果顯示,本文的演算法會明顯優於泰勒級數演算法與混合線演算法。以下列出泰勒級數演算法與混合線演算法的數學式:
在不失一般性的情形下,假設行動定位裝置鄰近的基地台有三個,三個基地台的位置分別為(0,0)、(X
2,0)與(X
3,Y
3)。則行動裝置與基地台的距離可以表示為:
以及相對於服務基地台的角度量測可以表示為:
Circle 1: x
2+y
2=r
12
Circle 2: (x-X
2)
2+y
2=r
22
Circle 3:(x-X
3)
2+(y-Y
3)
2=r
32
Line 1:
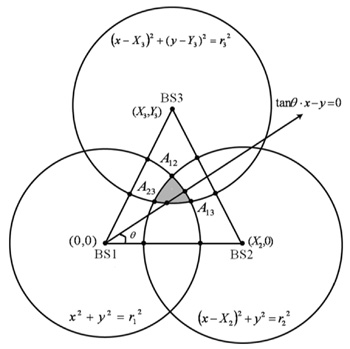 |
| 圖1 三圓一線的幾何示意圖 |
如圖1所示,一般來說,如果沒有非視距誤差,這些圓與線會交會於正確行動台位置上,但實際上非視距效應始終存在。由於非視距效應,訊號無法以直線距離傳輸,而量測到額外的距離,會對抵達時間造成正值的誤差;而對於抵達角度會造成角度偏移。但非視距效應始終存在,抵達時間無法測量到直線視距的真正距離,量測距離會永遠大於真實距離,因此可以預期,真正的行動台位置會座落在這些已抵達時間形成的圓的交集中,所以估測的行動台位置一定會滿足下列三個不等式限制:
值得一提的是,由於行動台的位置一定會落於三圓交集的部分,也就是圖1部分的A12A23A13,因此合理的角度線一定得通過三圓的交集部分,所以會對不通過三圓的交集之角度線進行適當的角度修正。數學式可以表示如下:
此外,在這裡提出了幾何分析法,以權重與排序的方法來分析這三圓一線在二維(2D)平面(幾何示意圖)上形成的交點。
| ‧ |
|
| |
步驟1將所有合適交點取平均值(XN,YN)。
步驟2計算各合適交點與平均值(XN,YN)的距離(di2)-1。
步驟3以(di2)-1為權重,求得估測位置。最後的行動台估計位置可以表示成:
|
| ‧ |
|
|
其步驟1與步驟2,與距離權重法的相同。然後,步驟3將合適交點,依照di的大小,以遞增進行排列。步驟4則以(di2)-1為權重,取前M個合適交點做平均值,獲得估計行動台位置
|
| ‧ |
|
| |
其步驟1計算兩兩合適交點間的距離dmn(1小於或等於m, n小於或等於N),接著步驟2選擇一個界限值Dthr,這裡取的是所有dm的平均值。步驟3則設定一個權重Ik,1小於或等於k小於或等於N,一開始起始值均為零。若dmn小於或等於Dthr,則將權重增加Im=Im+1、In=In+1(1小於或等於m, n小於或等於N)。步驟4為最後的行動台估計位置可以表示成:
|
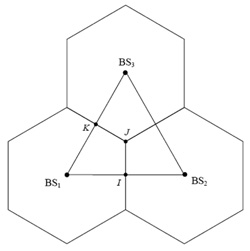 |
| 圖2 細胞配置圖 |
無線定位應用日益普及
電腦模擬基於以下不失一般性的假設:三個基地台的座標設為(0,0)、(1732m,0)與(866m,1500m),而行動台的位置則隨機坐落於服務基地台所服務的範圍內,I、J、K與基地台1所形成的區域內(圖2),模擬結果在每種情況取10,000次的數值運算後分析。附帶一提,在模擬結果中,排序權重的平均數取的是4.7,而界線值法的界線取的是9.2。
第一個誤差模型稱作CDSM,CDSM模型假設基地台與行動台的傳輸間存在一個散射點,此散射點坐落於行動台周圍的某個半徑上;由於散射點的干擾,抵達時間與抵達角度都會有所誤差。量測誤差則是存在一種分布,誤差高的機率較低、誤差小的機率較高。
用累積機率分布圖來看,圖3顯示的是一個累積機率曲線圖,假設在訊號傳輸時,由於行動裝置較靠近服務基地台,服務基地台的誤差較小,取其散射半徑為100公尺,而其他兩個基地台為400公尺,可以發現三種幾何法的表現皆遠優於上述的兩種相關定位法。
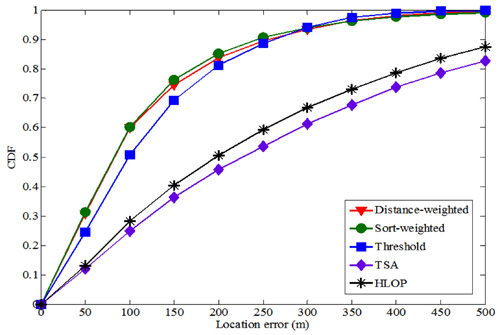 |
| 圖3 三圓一線在CDSM模型下的累積機率分布圖 |
除了累積機率分布圖外,亦可使用均方根誤差比較進行分析。假設服務基地台的散射半徑為100公尺,而其他兩個基地台的散射半徑則分布在100500公尺間,各種演算法的均方根誤差值分布圖可以表示成圖4,三種幾何法的均方根誤差值均遠小於傳統兩種定位演算法。
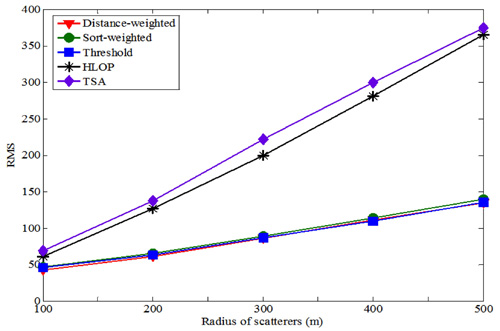 |
| 圖4 三圓一線條件在CDSM模型下,不同方法下的均方根誤差比較 |
筆者曾經於本雜誌2012年3月號提及兩圓兩線的幾何分析法,提供行動台只能偵測到兩個基地台時,藉由抵達角度量測的輔助的定位演算法。由於時間量測的精確度較高,此篇提出了若有三個基地台能夠提供抵達時間的量測,與最近的服務基地台能提供抵達角度量測時,同樣利用幾何分布產生的交點進行運算。以下用第二種誤差模型,比較此篇的方法與套用至兩圓兩線模型下的方法優劣。
第二種誤差模式稱做均勻分布模型,其誤差模型假設量測時間的誤差為均勻分布於(0,Ui),其中Ui又稱作量測時間的誤差上限;而抵達角度誤差則是假設為
wi為均勻分布函數於[-1,1]。在這一段,將三圓一線與兩圓兩線兩種情形,用累積機率分布圖來表示,其中Ui=200m、U2=U3=300m、t1等於5度與t2等於10度。如圖5所示,從中可以發現,這些方法中,三圓一線的定位精準度,會略勝於二圓二線;而在同一種情形下,提出的演算法會永遠較其他兩個相關演算法,提供較高的精準度。
 |
| 圖5 各種方法在兩種情況下之累積機率分布圖的比較 |
(本文作者依序為台南科技大學網路與資訊中心主任、國立成功大學電腦與通訊研究所研究生、高雄應用科技大學資訊管理研究所研究生)