人工神經網路(ANN)在機器學習和深度學習中占了重要的一部分,從由少數神經元組成的早期網路,到具有數千億參數(例如GPT-3)的新型網路,儘管ANN取得了顯著的成功,但人們仍然能從生物系統中學習,因為這些系統已經發展出各種驚人的解決方案,來解決人工智慧工程師所面臨的挑戰。
ANN早期受到生物學和人腦的啟發。第一個ANN稱為邏輯臨界值單元(Logical Threshold Unit),甚至被認為是「大腦網路」的一個簡單模型。1958年,心理學家Frank Rosenblatt提出了感知器,這是監督學習的早期演算法,也是生物神經元的簡化模型,儘管受到一些挫折,如由Marvin Minsky和Seymour Papert於1968年出版的爭議性著作《感知機》(Perceptrons)一書引發的爭議,但自此以後,感知器一直保持著穩定性,並支撐了現代人工智慧的驚人進步。
然而,儘管它們有其共同的起點,但人工智慧和生物研究界卻存在歧異,對神經網路的理解也變成特定社群專屬,雖然有些ANN能更直接地從生物學中獲得靈感,例如脈衝神經網路(Spiking Neural Network, SNN),但人工智慧為ANN開發的基本工具,如透過誤差反向傳播進行學習,似乎在生物神經網路中就沒有直接的相似物。
現代人工智慧的成功,特別是深度學習,證明了過去60年來神經網路研究所開發工具的驚人實用性。然而,有鑑於生物學以不同的方式進行研究,人們必須探究是否還可從大自然中學習甚麼,以進一步擴展人工智慧的能力。
文獻中經常看到的一種模式,是奠基於生物學上更合理的ANN副作用,為提升效率(記憶體、執行時間、超參數調整等),同時達到最先進的性能,這在多個數據集、指標、網路架構和任務中,都可以觀察到其暗示了開發受生物啟發之ANN的主要益處。
為了保持文獻綜述範圍可控,以下先確定了三個主題(但這並非詳盡無遺):
.梯度下降反向傳播的替代演算法
.網路架構的替代方案
.啟動函數和注意力機制的替代機制
本文將文獻搜尋縮小到圖1所示的範圍。
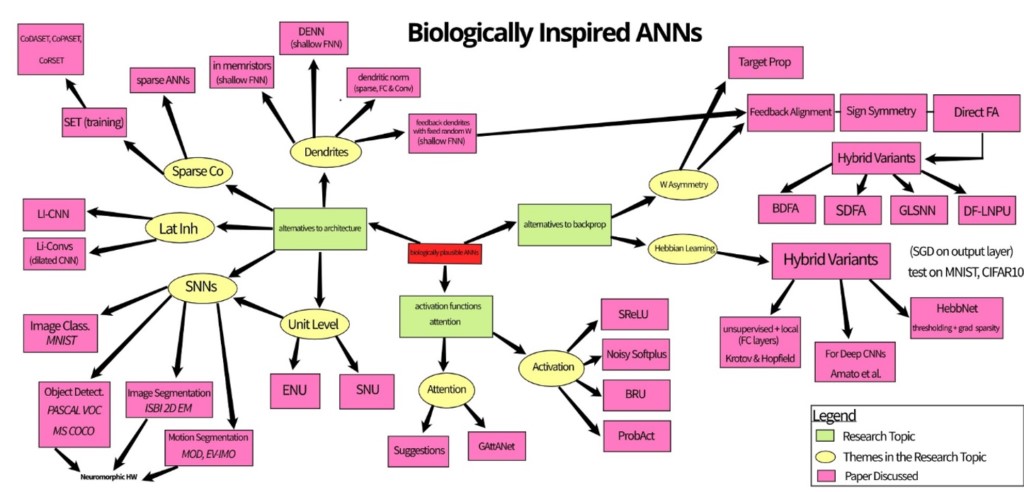 圖1 關於ANN生物合理性三個研究主題的思維圖
圖1 關於ANN生物合理性三個研究主題的思維圖
替代方案反向傳播
自1980年代反向傳播(Backpropagation)普及以來,研究人員已經多次嘗試尋找學習的替代方法,通常是從生物學中尋找靈感。 在討論這些受生物啟發的替代方案之前,以下簡要地談談反向傳播在生物神經網路中被認為不可信的兩個主要原因。
.權重傳輸問題:
在此需要將前向傳遞的權重「傳輸」給後向傳遞,以便進行權重更新計算,其中本文使用了前饋權重矩陣的轉置W,生物神經網路中沒有已知的機制允許權重從前向反饋傳遞到後向傳遞。
.更新鎖定問題:
在反向傳播中,權重更新僅在完全前向饋傳遞後發生。大腦中反饋訊號的時間與反向傳播訓練的ANN不同,它們因生物神經網路而異,例如參見錐體神經元及其頂端樹突。在整個大腦中,學習的反饋是什麼樣子?目前尚無一個通用而精確的定義。
(一)赫布學習
赫布學習(Hebbian Learning, HL)的直接靈感來自早期關於人類學習和大腦神經可塑性的生物實驗。如今,它有許多變體,在神經科學界接受程度不同,但這個規則的第一個表述可以追溯到1949年的「赫布定律」,它是一種無監督的學習規則,並被認為是生物學習的基礎或最簡單的敘述。
赫布定律實現的一個局限是無限成長的問題,因此,在整個訓練過程中,權重會無限期地呈指數級成長,加強神經元之間的連接,會增加放電頻率,進而加強聯繫,形成失控的正反饋回路(圖2)。
 圖2 兩個相連神經元的簡化圖(由Dana Scarinci Zabaleta繪製)
圖2 兩個相連神經元的簡化圖(由Dana Scarinci Zabaleta繪製)
最近一篇使用赫布定律的論文是學者如Manas Gupta等人於2021年完成的工作,名為「赫布網路(HebbNet)」,主要便是試圖解決此無限成長的問題。
赫布網路是一個淺層全連接神經網路,有一個2,000單元的隱藏層,輸出層的權重使用梯度下降法更新,而隱藏層訓練是透過三個類似赫布學習定律之一實現的:最簡單的版本(赫布定律)為帶臨界值的赫布定律;或帶臨界值和梯度稀疏性的赫布定律,不過並非所有權重矩陣元素都在每次後向傳遞時更新。
還有其他方法可以解決赫布定律中無限成長的問題,如奧賈(Oja)定律和Henry Markram等學者於1997年提出,主要用於脈衝神經網路的尖峰時間依賴可塑性(Spike-timing-dependent Plasticity, STDP)。奧賈定律是個數學公式,透過導入一個「遺忘」的術語來解決無限成長的問題。在圖3中,可以看到在赫布網路論文的設定中,將赫布定律替換為奧賈定律時輸出了結果。
 圖3 赫布網路實驗中MNIST和CIFAR-10的測試精度
圖3 赫布網路實驗中MNIST和CIFAR-10的測試精度
(HL=赫布學習;T:臨界值;GS:梯度稀疏)
在此試圖重現赫布網路論文的結果,並與奧賈定律比較。圖3顯示MNIST和CIFAR-10上的測試精度。請注意,筆者使用的超參數配置與論文中相同,除了學習率(避免權重增長失控導致的浮點溢出)和梯度稀疏性(將其固定為p=0.3,即每次向後傳遞時僅更新30%的權重矩陣,而論文提到使用最佳值)以外。
不出所料,原始配方「Vanilla」無論使用何種規則,HL在MNIST分類中的表現都很差,但令人驚訝的是,對於CIFAR-10分類,赫布學習的三個不同版本的表現都相似。可以注意到,呈現的結果遠遠低於論文中報告的結果。此外,在本文提出的實驗中,奧賈定律通常優於赫布定律。 在HebbNet論文中,赫布學習和帶梯度下降的反向傳播分別用於不同層的訓練:前者用於隱藏層,後者用於輸出層。這使得在監督訓練期間很難提倡使用赫布學習,因為相較之下,反向傳播適合網路中所有層的訓練。在一個網路採用兩種學習方法,反倒不利且增加了其複雜性。
有鑑於此,本文研究了如何用相同學習演算法/規則訓練淺層、完全連接的神經網路的所有層。首先,為了用一個隱藏的層來訓練同一個網路,便透過添加無監督的赫布學習定律,修改了反向傳播中傳統梯度的定義,即梯度成為以下簡單的「求和規則」:
梯度=反向傳播梯度+β*赫布學習定律(赫布或奧賈定律),其中β為比例因數(例如,β=10e-2)。
在此使用赫布或奧賈定律,在簡單梯度下降和赫布學習更新中訓練網路。
而圖4顯示了赫布學習比例因數β的測試精度,其中使用的是赫布定律。
 圖4 MNIST和CIFAR-10的測試精度(求和規則)
圖4 MNIST和CIFAR-10的測試精度(求和規則)
對於MNIST來說,奧賈定律導致測試精度降低(約30%);對於CIFAR-10,使用奧賈定律的結果與圖4中赫布定律顯示的結果類似。
在這兩種分類任務中,赫布學習的貢獻越小,測試精度越高。在比例因數越小的情況下,使用此求和規則獲得的測試精度,與在兩個數據集上使用反向傳播獲得的性能相匹配。這些結果說明,以這種方式添加赫布學習元件,不會降低測試精度相對於反向傳播的任何好處。
文獻中也記錄了提出單一學習規則的嘗試。2019年,有學者如Jan Melchior與Laurenz Wiskott提出了「赫布下降(Hebbian Descent)」,這是一種受生物學啟發的學習規則,可用於監督和無監督的學習。
本文特別關注監督學習場景,在該場景中,便加以研究了MNIST和CIFAR-10上淺層全連接網路(與HebbNet相同)的分類性能。
本文同時也研究了將更新規則中的核心輸入因數替換為奧賈定律。圖5顯示了MNIST和CIFAR-10的測試精度,其中BP指的是反向傳播。有三個訓練版本:全部(隱藏層和輸出層權重均已更新)、第一部分(隱藏層權重已凍結)、第二部分(輸出層權重已凍結)。
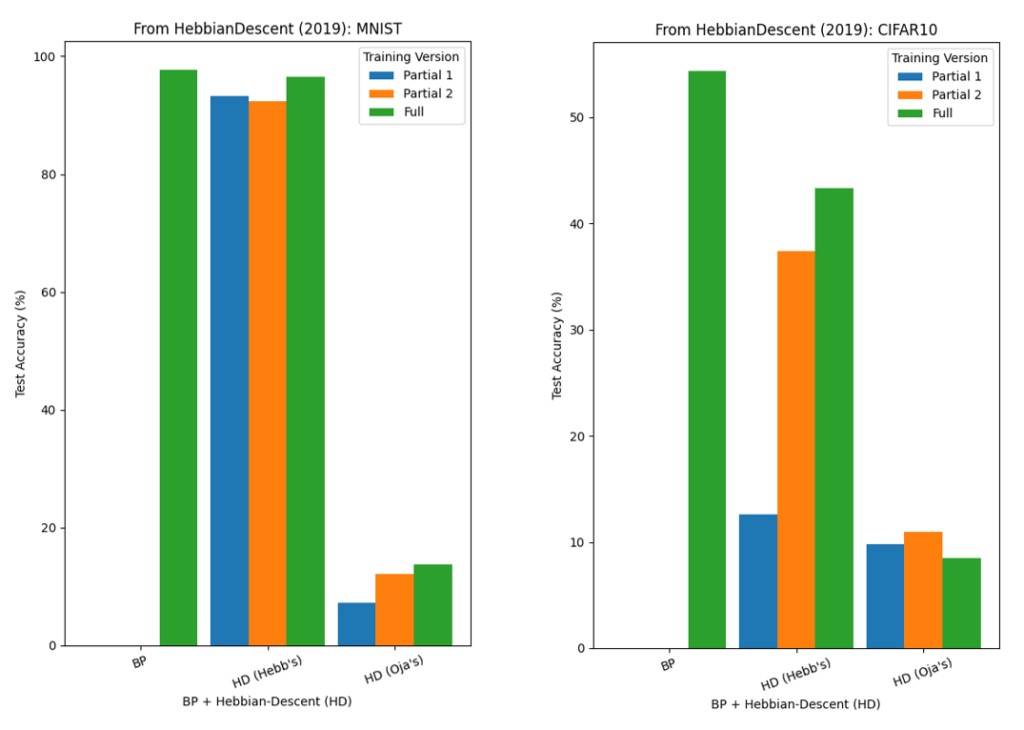 圖5 赫布理論實驗中MNIST和CIFAR-10的測試精度
圖5 赫布理論實驗中MNIST和CIFAR-10的測試精度
儘管赫布下降在MNIST上的表現非常相似,但反向傳播在兩個數據集上的表現都優於赫布下降。此外,在MNIST上,在所有層上執行赫布下降似乎沒有什麼優勢,而僅在某些層上執行(部分在CIFAR-10上未觀察到的結果:這可能是因為MNIST比CIFAR-10更容易,因為在CIFAR-10中,凍結權重不會妨礙分類。在這兩個數據集上,使用奧賈定律的修改規則都落在後面。
綜上所述,赫布學習(赫布定律、奧賈定律)的簡單變體似乎與傳統反向傳播網路的精度不匹配,最有希望的結果(接近反向傳播水準)是在與梯度下降(例如2019年Melchior與Wiskott提出的赫布下降)結合時獲得的。本文懷疑,赫布學習的較新變種可能表現更好,例如尖峰時間依賴可塑性,還有多種其他學習規則源自赫布定律。在所有情況下,簡單的赫布學習變種似乎是全部,它們可能更有效地成為更複雜的學習規則,或用於具有特定配置的訓練網路的一部分,例如用於脈衝神經網路的STDP規則。
(二)回饋校準方法
2016年,社群推出了一組名為反饋校準(FA)方法的學習演算法,用於處理權重傳輸問題,最初的反饋校準演算法由Timothy P. Lillicrap等學者於2016年記錄,同年晚些時候,Arild Nøkland提出了一項名為「直接反饋校準(DFA)」的擴展。
這個想法很簡單,兩種演算法都使用固定隨機矩陣作為反饋權重矩陣,本質上,前饋權重矩陣W(WT)的轉置變為B,其中B是訓練前定義的固定隨機矩陣。這樣,便不需要儲存和使用前饋權重的轉置。DFA比FA更進一步,使用輸出層的梯度而不是來自更高級別隱藏層的梯度更新網路的早期隱藏層,如圖6所示,藉以視覺化這些演算法(BP:反向傳播)。
 圖6 兩個隱藏層、完全連接的神經網路上的訓練演算法(2016年,Nøkland)
圖6 兩個隱藏層、完全連接的神經網路上的訓練演算法(2016年,Nøkland)
接下來,本文則使用FA(圖7)或DFA(圖8)進行訓練的網路的分類結果,為300個週期:這些網路有一個隱藏層(2,000個單位:ReLU)或兩個隱藏層(每個800個單位,ReLU/Tanh層,其具有偏差)。
 圖7 FA實驗中MNIST和CIFAR-10的測試精度
圖7 FA實驗中MNIST和CIFAR-10的測試精度
 圖8 DFA實驗中MNIST和CIFAR-10的測試精度
圖8 DFA實驗中MNIST和CIFAR-10的測試精度
以下嘗試了四種方法來定義反饋矩陣B。
1.固定隨機:如2016年關於FA和DFA的論文中所述。
2.固定隨機(符號):與固定隨機矩陣類似,但此處符號在每次傳遞時與前饋矩陣W一致,類似另一種稱為「符號對稱」的演算法。
3.固定二進位:B是隨機選擇-1和1的固定矩陣。
4.二進位(符號):B是1的矩陣,在每次傳遞時,該符號與前饋矩陣W全等。
FA和DFA的結果不如赫布學習結果清晰,事實上,在某些情況下,他們的表現優於反向傳播,但選取清晰模式可能很複雜:學習方法和反饋矩陣B對測試精度的影響高度依賴於所使用的網路(隱藏層的數量、啟動)和數據集。
關於上述反向傳播結果,也有注意到缺乏過度擬合。此外,在運行了五次訓練後,接著檢查在MNIST1隱藏層場景中,訓練精度和測試精度樣本內的標準偏差是否為零。
(三)赫布學習×回饋校準
最後,則結合了FA方法和赫布學習進行實驗,因此有:
1.反向傳播/FA,其中其中使用赫布學習(赫布或奧賈定重矩陣B:HL×FA。
2.DFA,其中使用赫布學習(赫布或奧賈定律)訓練反饋權重矩陣B:HL×DFA。
有鑑於本文利用兩個受生物學啟發的概念來學習單個網路,這種結合尤其有趣。而在許多學者已發布的文獻資料中,也記錄了這一點作為未來研究的建議,或是其他將赫布學習變體和反饋一致性聯繫起來的嘗試也已經公開發表。
對於使用上述反向傳播/FA的實驗,請參閱圖9和圖10。
 圖9 Hl✕Fa實驗中對MNIST的測試精度(左:赫布規則;右:奧賈規則)
圖9 Hl✕Fa實驗中對MNIST的測試精度(左:赫布規則;右:奧賈規則)
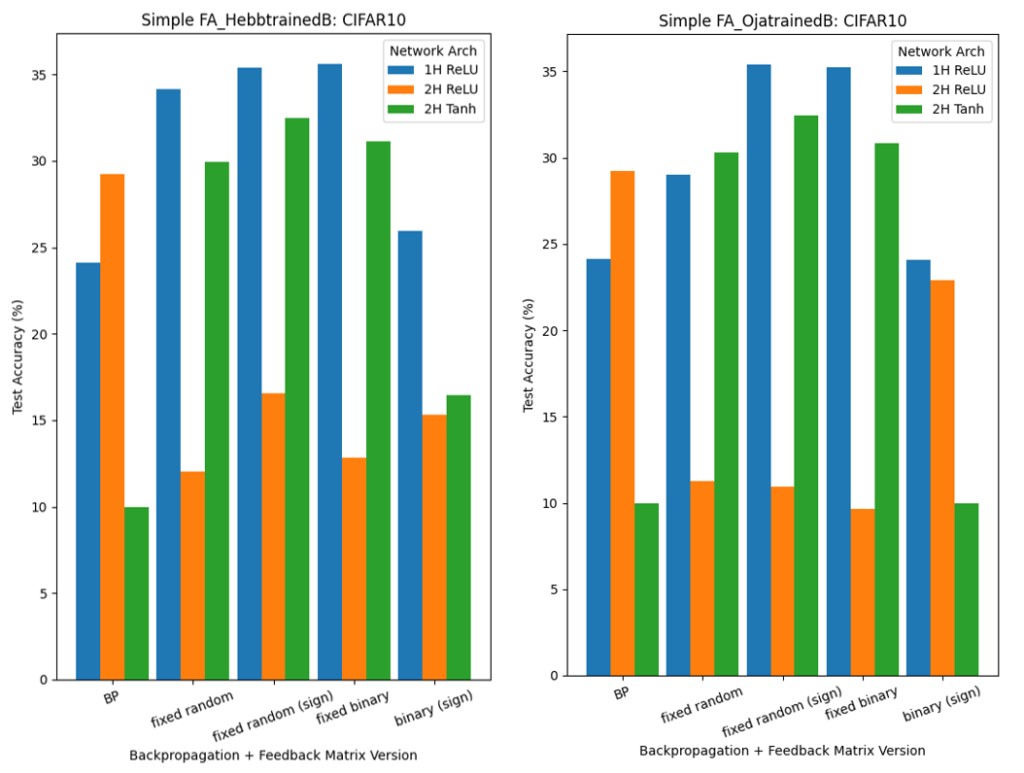 圖10 Hl✕Fa實驗中CIFAR-10的測試精度(左:赫布規則;右:奧賈規則)
圖10 Hl✕Fa實驗中CIFAR-10的測試精度(左:赫布規則;右:奧賈規則)
圖11顯示了使用DFA訓練時的結果,並帶有可訓練的B矩陣。在這種情況下,無法直接使用奧賈定律:其實依賴於與前饋權重W形狀相同的張量,而在DFA中,早期隱藏層的反饋權重矩陣,其形狀有所差異,以適應正在使用的輸出層梯度。
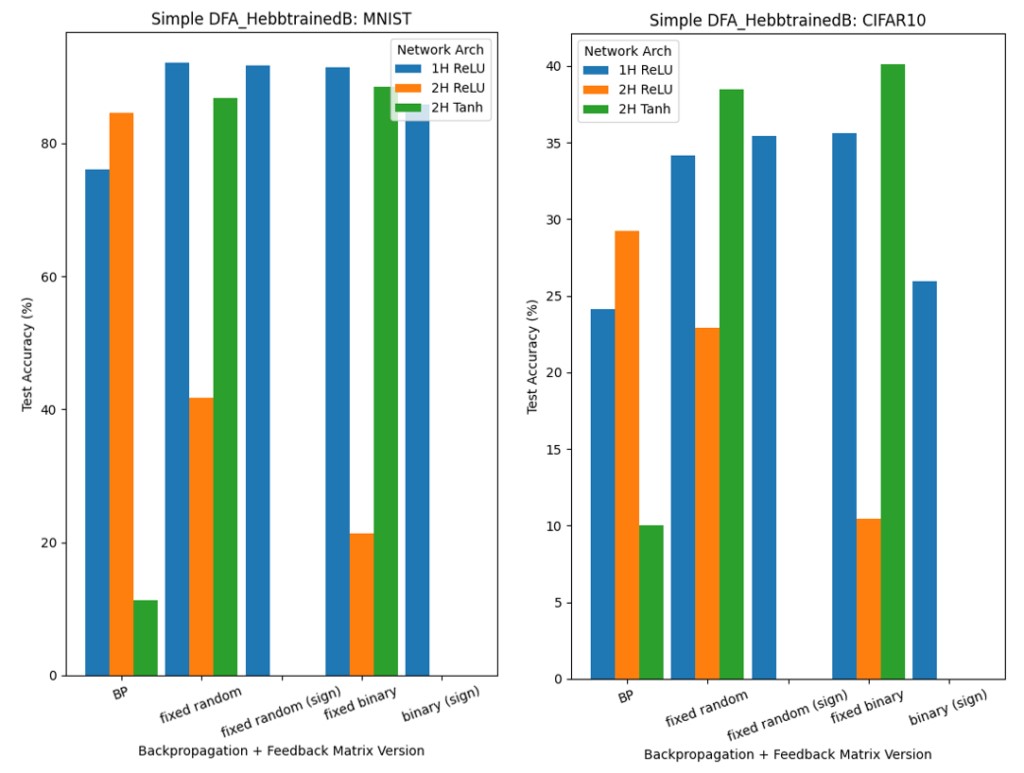 圖11 HL✕FA實驗中MNIST和CIFAR-10的測試精度(赫布規則)
圖11 HL✕FA實驗中MNIST和CIFAR-10的測試精度(赫布規則)
巧用生物學習研究人工神經網路
本文對具有不同程度生物學靈感的人工神經網路進行了文獻綜述。有鑑於已發表的大量工作,特別是在過去十年中,人工智慧中的生物合理性主題肯定會繼續受到研究界的關注。重要的是,除了理論、學術界對連接人工智慧和神經科學的興趣之外,在人工智慧產業環境中,反思生物學靈感也具有很大的潛力。首先,越來越多的研究出版物調查在專業硬體上訓練生物啟迪的人工神經網路,這可能會引起業界的興趣。其次,幾篇論文也指出了在訓練中的提高(儲存、執行時間),即使測試精度接近、或處於反向傳播訓練網路的水準。
從本文的赫布學習和反饋校準結果中可以注意到,大多數情況下,反向傳播是贏家。然而,也有一些情況下,其他演算法接近反向傳播的性能水準,尤其是FA方法。
這不應阻止針對生物學啟迪的人工神經網路進行進一步研究。在這裡,本文只研究了一個參數,即學習方法。很可能是使用的網路的所有其他參數/特徵都有反向傳播偏差,在這種情況下,便可能低估了生物學習的真正潛力。因此,採取多維和詳盡的方法進行進一步的工作是必要的,例如透過查看卷積層等方式。最後,各界也注意到,最近的論文越來越頻繁從多個層面研究生物合理性,例如,在具有生物啟發功能的網路架構上使用生物學習規則,而本文則懷疑這說明了未來生物學研究對AI的影響。
(本文作者任職於Imagination)