在無線通訊運用上,功率放大器(Power Amplifier, PA)電路設計的基本考量為線性度及效率的問題。考慮發射端,功率放大器的線性度影響到訊號的輸出品質,而效率則決定了電池使用及待機時間的長短。一般而言,這兩項參數是互相抵觸的,所以如何在線性度與效率之間做取捨,是設計製作功率放大器的重要指標。
在實際運用功率放大器時,必須考慮到訊號的調變方式。舉例來說,全球行動通訊系統(GSM)採用GMSK的調變方式,訊號振幅是常數,可容許功率放大器有較大的失真以追求功率效益,但在頻譜效益(Spectral Efficiency)就比較差;長程演進計畫(LTE)則採用正交分頻多工(OFDM)的調變方式,雖然在頻譜效益的表現很好,但訊號振幅的變化很大,對功率放大器的線性度要求就比較高,或者須回退(Back Off) 1-dB壓縮點來工作,造成功率效益極差。
一般無記憶非時變(Memoryless, Time-invariant)的非線性電路,通常都可以使用有限項次的泰勒級數(Taylor Series)來表示,其輸入𝑣𝑖與輸出𝑣𝑜關係式如公式1所示[1]:
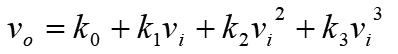
.......................公式1
例如,交流電(AC)/直流電(DC)轉換只關心𝑘₀,線性的衰減器或放大器只需要𝑘₁,利用𝑘₂可以完成混波(Mixing)或頻率轉移(Frequency Conversion)的功能,利用𝑘₂或𝑘₃可以做成兩倍或三倍的倍頻器(Frequency Multiplier),但是,對要求線性的放大器來說,除了𝑘₁之外,其他都只會造成干擾,尤其是公式1中的𝑘₃,造成的影響通常會落入帶通(Passband)頻段內。𝑘₃是本文的主角,它決定三階截斷點(3rd-order Intercept Point, IP3)及1dB壓縮點,後續會仔細討論。
對於一般的弱非線性功率放大器來說,AM-PM的失真通常可以忽略,若只針對AM-AM來做討論,則三階多項式近似法是一種可行的模式,考慮一個弱非線性功率放大器,假設輸入為單一頻率𝑓₁之訊號,𝑣𝑖(𝑡) = 𝐴𝑐𝑜𝑠(2𝜋𝑓₁𝑡) = 𝐴𝑐𝑜𝑠𝜔₁𝑡,代入上式後,可得到輸出訊號如公式2所示。

.......................公式2
由公式2可知輸出訊號是由基頻(Fundamental)頻率𝑓₁、二倍頻率2𝑓₁及三倍頻率3𝑓₁所構成,後兩者並非輸入頻率的訊號,也稱做諧波(Harmonics)。觀察基頻項可以知道電壓增益,如公式3所示。
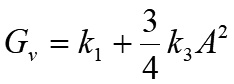
.......................公式3
通常的放大器電路之𝑘₃<0,所以當輸入訊號振幅(𝐴)變大,其增益會降低,此效應稱作增益壓縮(Gain Compression)或飽和(Saturation)。圖1是一個真實功率放大器的量測結果,可以清楚地看到增益壓縮的現象。當增益壓縮達到1dB,其所對應的輸入功率稱做輸入端的1dB壓縮點(1dB Compression Point),透過電腦模擬,當輸入功率超過1dB壓縮點3dB(兩倍),公式1都還適用,若超過太多,不但公式1無法使用,此功率放大器很可能燒壞了。
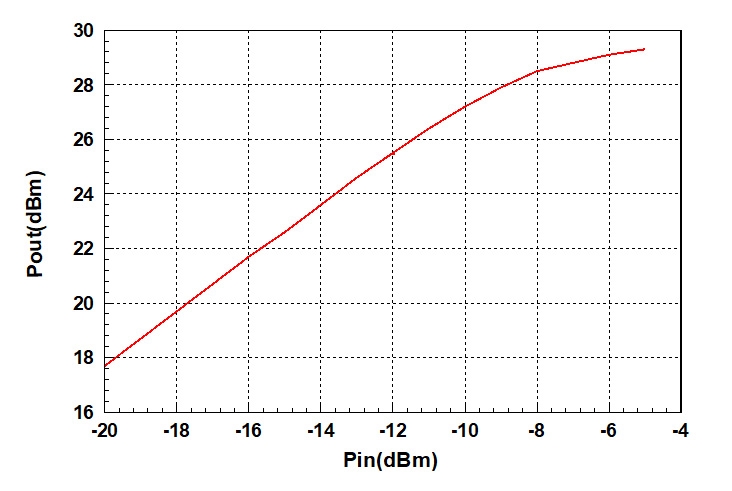 圖1 功率放大器輸入與輸出功率量測圖
圖1 功率放大器輸入與輸出功率量測圖
三階截斷點與1dB增益壓縮點
為了方便討論,這裡先定義截斷點(Intercept Point, IP)。如圖2所示,其中的IP3即是三階截斷點(3rd-order Intercept Point, IP3)。觀察圖2,當輸入功率慢慢增加,輸出的基頻與3倍頻也會線性的增加,輸入功率增加1dB,基頻輸出也會增加1dB,然而3倍頻輸出卻增加3dB,這是屬於線性區。若輸入功率再繼續增加,最後兩者都會進入飽和區。
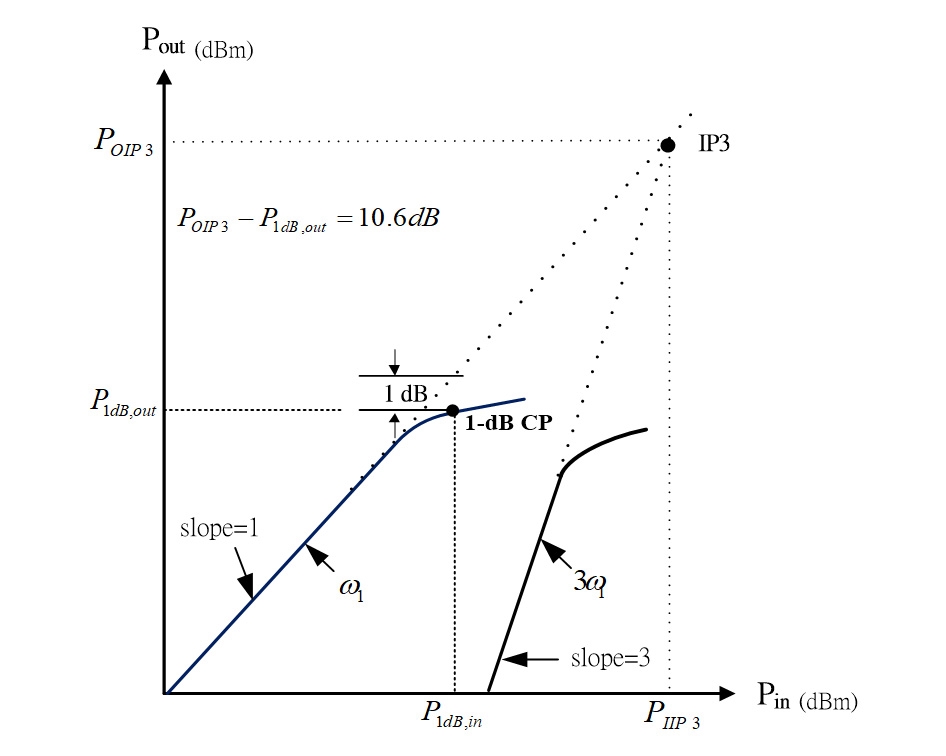 圖2 1dB增益壓縮點與三階截斷點(IP3)之示意圖
圖2 1dB增益壓縮點與三階截斷點(IP3)之示意圖
如果以想像的方式將線性區延續,則最後兩直線(圖中的虛線)會交會於一點,此虛擬的交叉點即是三階截斷點。換句話說,IP3的定義為基頻輸出和3倍頻輸出的假想直線部分之延伸相交於一點,即為三階截斷點,如圖2所示。特別注意IP3與輸入訊號強度無關,因此可以當作客觀的線性度指標。就像北極星,雖然我們到不了,但可以指引夜間的方向。
由於非線性效應的關係,放大器在小訊號時,輸入功率與輸出功率呈線性關係。但是,當輸入訊號超過一特定功率值後,輸入與輸出功率的關係將不再是線性,使得功率增益被壓縮,如公式3所示。當實際的輸出功率比線性輸出功率小1dB時,則稱此點為1dB增益壓縮點(1dB Cmpression Point),如圖2所標示的。
假設公式1是正確的,經由推導可以得到輸出𝑃𝑂𝐼𝑃3與𝑃1𝑑𝐵,𝑜𝑢𝑡的關係則如公式4所示[2]:

.......................公式4
一般A類(Class A)放大器大約都遵循公式4,其他的非線性元件,例如混波器(Mixer),兩者差值可能會到12至15dB。
討論至此,理論上靠著單頻(Single Tone)量測1倍頻與3倍頻的輸入/輸出關係即可推算出IP3,但存在著一個大問題,例如考慮一個5GHz的微波放大器,其輸出端一定會針對5GHz做匹配電路,此時3倍頻15GHz輸出的增益已經不是正確的,這時得到的IP3當然是錯的。換句話說,通常的放大器後端會加上調諧電路或濾波器以抑制二次及三次諧波,所以單頻測試通常是行不通的,底下討論的雙頻測試(Two-tone Test)就可以解決IP3量測的問題。
雙頻測試與交互調變失真
如果輸入是兩個頻率很相近的訊號(公式5),例如實際通訊時兩個相鄰頻道的訊號,則輸出結果如公式6所示。
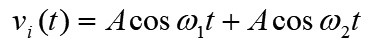
......................公式5
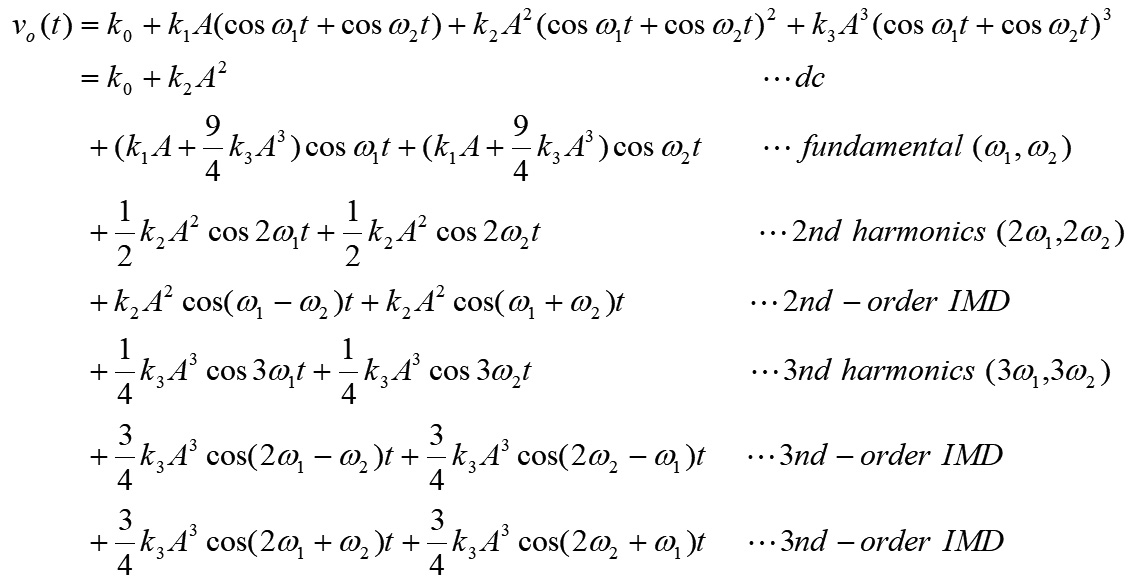
......................公式6
輸出訊號的頻譜是由𝑓₁、𝑓₂、2𝑓₁、2𝑓₂、𝑓₁±𝑓₂、2𝑓₁±𝑓₂、𝑓₁±2𝑓₂等等頻率所組成,2𝑓₁和2𝑓₂為二次諧波,𝑓₁±𝑓₂則是二階交互調變失真(Intermodulation Distortion, IMD),而2𝑓₁±𝑓₂和𝑓₁±2𝑓₂為三階交互調變失真。 考慮一般的發射機,因為二階或更高偶數階的交互調變失真,其頻率與主頻率相差很大,可以用濾波器濾掉,所以較不考慮它的影響。但是,三階或奇數高階交互調變失真和主頻率幾乎相同或接近,只相差|𝑓₁−𝑓₂|的等級,難以用濾波器濾除,影響就很大了。圖3為交互調變失真頻譜示意圖。
在無線通訊的領域裡,因為以三階交互調變失真的影響最大,因此通常只考慮三階截斷點的大小。基本上,IP3的位置愈高,電路受三階交互調變失真訊號的影響愈小。
 圖3 交互調變失真頻譜示意圖
圖3 交互調變失真頻譜示意圖
進行IP3量測 - 雙頻測試
量測IP3可在放大器的輸入端輸入兩個功率相同,大小適當且頻率相近的𝐴𝑐𝑜𝑠𝜔₁𝑡與𝐴𝑐𝑜𝑠𝜔₂𝑡訊號,在輸出端可測得位於2𝑓₁−𝑓₂或2𝑓₂−𝑓₁之訊號功率,由於它們與𝑓₁或𝑓₂接近,因此不受輸出端匹配電路的影響。透過公式6中2𝑓₂−𝑓₁與𝑓₂的振幅及功率關係,經由數學推導可以求出𝑃𝑂𝐼𝑃3,如公式7所示[3]。
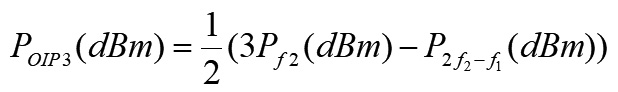
......................公式7
利用公式7並配合儀器操作,可以整理出射頻放大器(RF Amp)之IP3量測步驟如下[3]:
首先,將訊號源接至射頻放大器之輸入端,放大器電路輸出端則接到頻譜分析儀(圖4)。
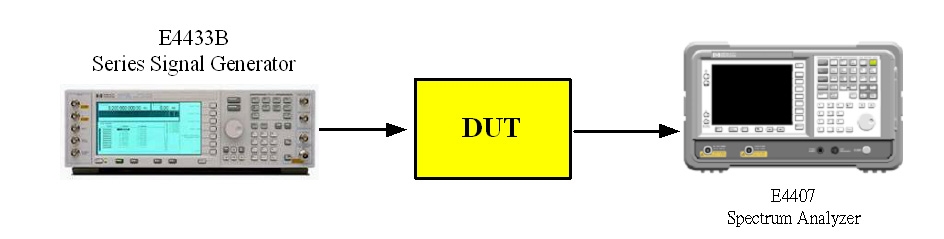 圖4 射頻放大器之P1dB與IP3測量圖
圖4 射頻放大器之P1dB與IP3測量圖
接著,設定數位訊號產生器ESG產生兩組訊號,其輸出功率相等並大小適當(切記不能太強),頻率分別為𝑓₁及𝑓₂(𝑓₁≠𝑓₂,但兩者非常接近)。
然後,觀察頻譜上是否有2𝑓₁−𝑓₂及2𝑓₂−𝑓₁訊號出現。
最後,稍微調整兩組訊號源的輸出功率,使頻譜上𝑓₁和𝑓₂訊號的強度相同(圖5),並以公式7計算出𝑃𝑂𝐼𝑃3的大小。計算結果如公式8所示。
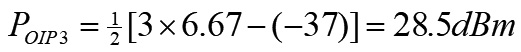
.......................公式8
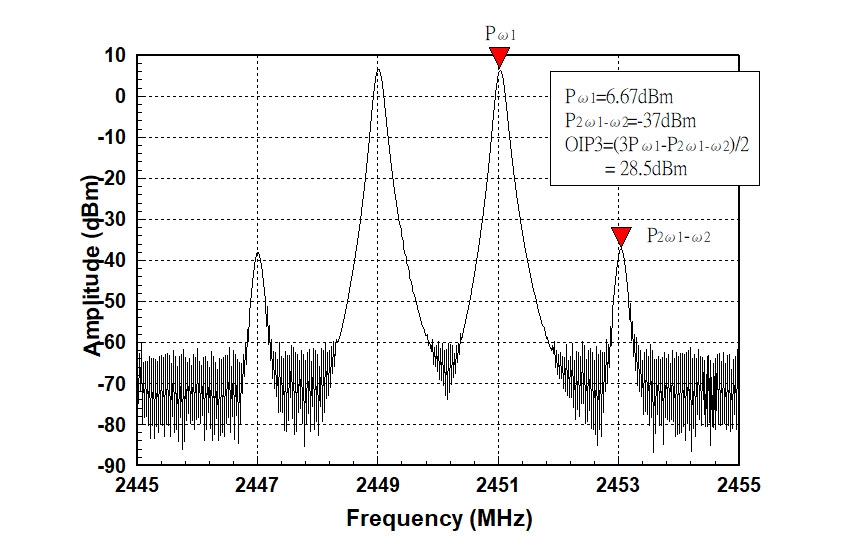 圖5 雙頻測試及三階截斷點計算
圖5 雙頻測試及三階截斷點計算
要特別提醒的是,在IP3量測時輸入端輸入的兩個相同功率值不可以太大,曾經有新手以為要量測IP3就要灌進很強的訊號使放大器進入飽和區,切忌這觀念是錯的。
IP3與數位調變訊號
上一節當中,已經介紹了非線性功率放大器在輸入端輸入兩個頻率相近的𝑓₁與𝑓₂訊號時,會因交互調變而產生難以用濾波器濾除的2𝑓₁−𝑓₂與2𝑓₂−𝑓₁頻率。若輸入為數位調變訊號時,三階交互調變失真的影響將包含原訊號的頻段內及鄰近通道(Channel),如圖6所示,此一部分的影響是很難用濾波器濾除。
在圖6中,數位調變訊號的三階交互調變失真可以拆解成三部分,中間區域稱為頻段內混疊失真(Inband Aliasing Distortion),直接讓數位調變訊號品質劣化,兩邊的區域稱為頻段外三階交互調變失真(Outband 3rd-IMD),此現象也稱作頻譜增生(Spectral Regrouth),會干擾鄰近通道。
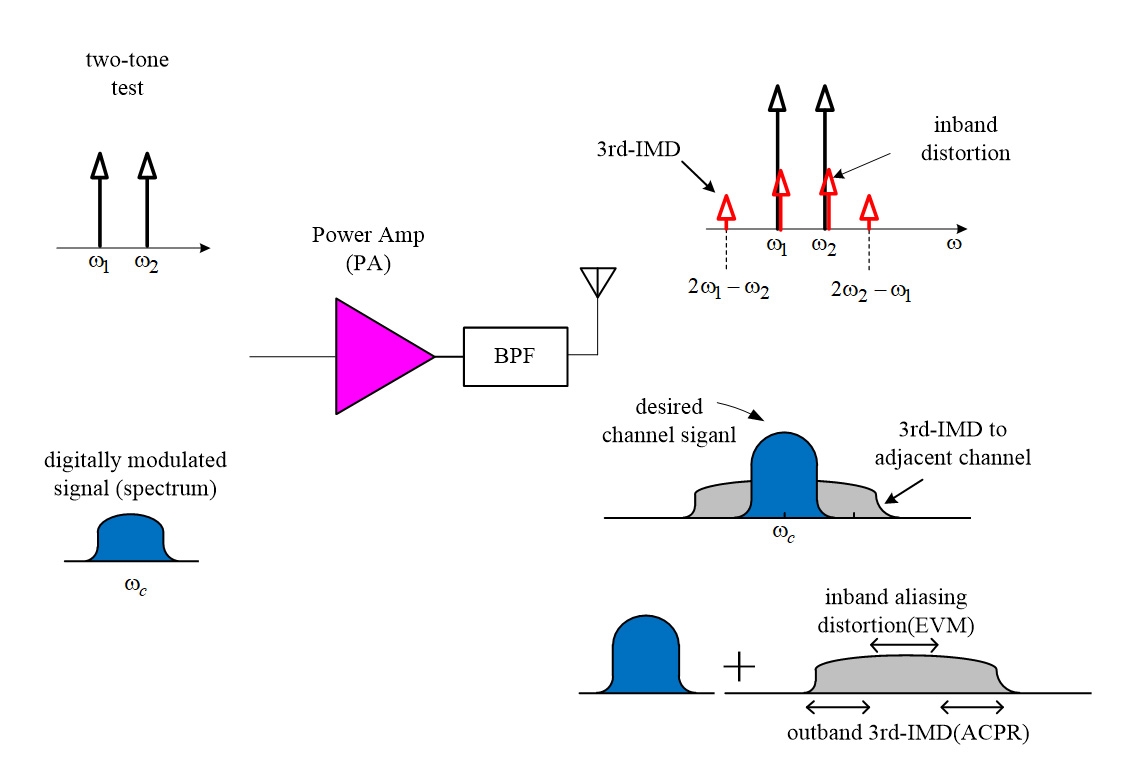 圖6 數位調變訊號受非線性放大器影響的示意圖[4]
圖6 數位調變訊號受非線性放大器影響的示意圖[4]
額外說明在圖6中,為什麼數位調變訊號的三階交互調變失真頻寬會是主通道頻寬的3倍。卷積(Convolution Integral)運算定義成,如 果v1(f)與v2(f)頻寬有限,分別是W1與W2,則卷積運算結果主要訊號頻寬會得到W=W1+W2。一個訊號的3次方,例如,根據傅立葉轉換(Fourier Transform)的理論,在頻譜上等於做的運算,運算結果在主通道附近就會產生3倍頻寬的三階交互調變失真。
下一節裡將以MATLAB程式模擬非線性功率放大器對數位調變訊號的影響。對於頻段內混疊失真使得調變訊號劣化,其劣化程度將以誤差向量振幅值(Error Vector Magnitude, EVM)的方式來做分析與評估,鄰近通道干擾則以鄰近通道功率比(Adjacent Channel Power Ratio, ACPR)做量化討論,最後並透過量測結果與模擬相互驗證。
先介紹W,在接收端的數位調變訊號,例如M-QAM或M-PSK這一類,都可以在I/Q平面上以星座圖來表示。由於受到非線性功率放大器的影響,因此在星座圖上的點將會偏離原參考點。此偏移的量,將以EVM做為評量的標準。EVM的定義如圖7所示,即圖中誤差向量(Error Vector)的大小。EVM的值通常為計算所有誤差向量的均方根誤差值(Root-mean-square, rms)。
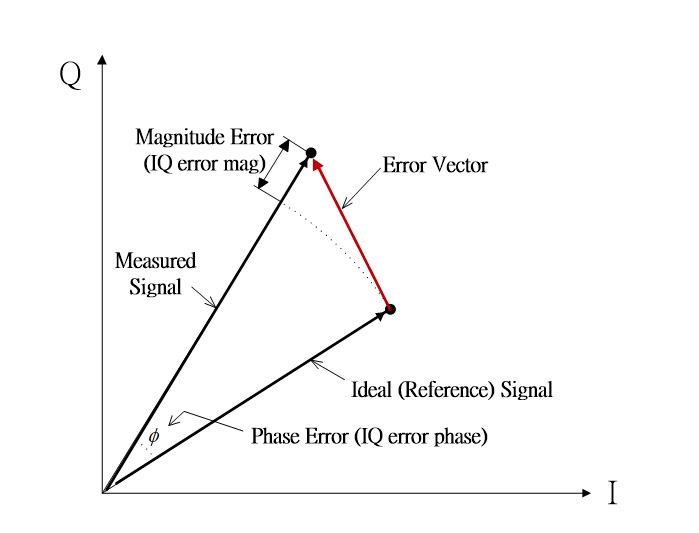 圖7 EVM示意圖
圖7 EVM示意圖
圖8為量測示意圖,包含向量訊號產生器(Vector Signal Generator)及向量訊號分析儀(Vector Signal Analyze, VSA),操作時要特別注意功率放大器的輸出是否超出VSA所能承受的最大輸入功率以避免燒壞儀器,為防意外,建議加上衰減器來保護VSA。圖9為VSA量測結果的輸出圖,可以看到EVM=5.4673%。
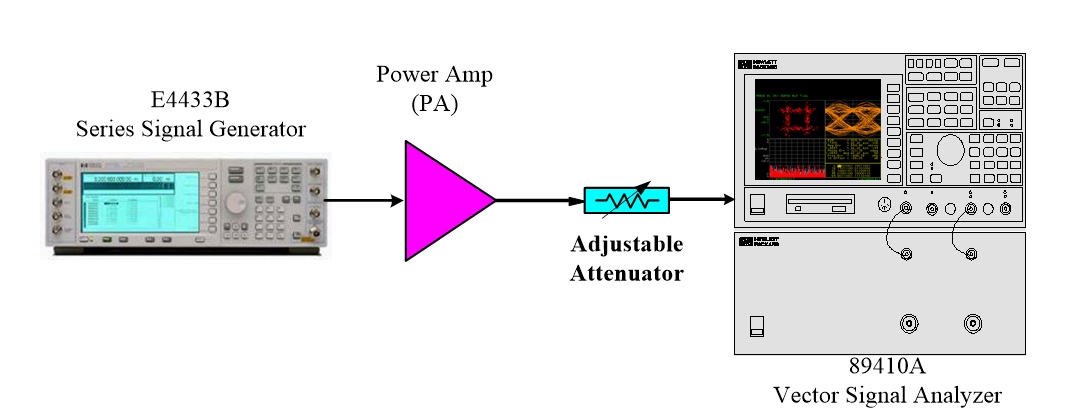 圖8 使用安捷倫ESG-D向量訊號產生器及VSA量測EVM示意圖
圖8 使用安捷倫ESG-D向量訊號產生器及VSA量測EVM示意圖
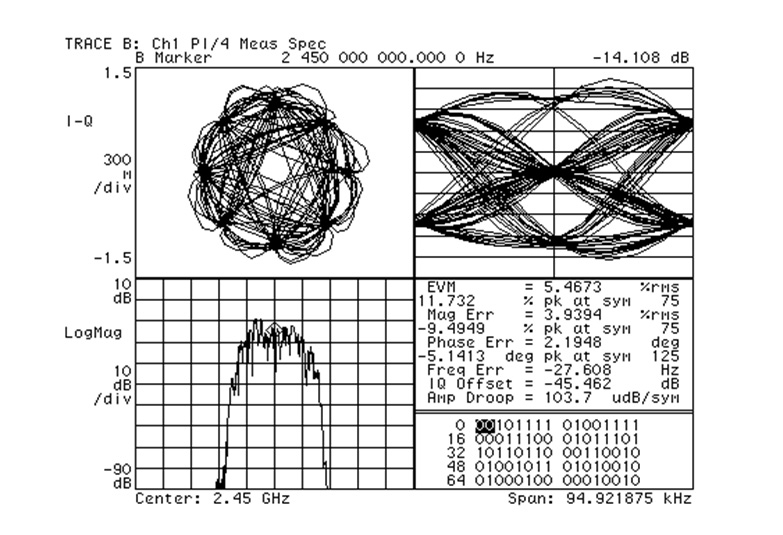 圖9 EVM量測結果舉例
圖9 EVM量測結果舉例
ACPR是定義成主通道功率(Main Channel Power)與鄰近通道功率(Adjacent Channel Power)的比值,通常以dB表示,如圖10所示,其中的縱軸單位是功率頻譜密度(Power Spectral Density, PSD)。鄰近通道功率是因為數位調變訊號經放大器產生的頻譜再生現象造成的。 ACPR是一種品質因數(Figure-of-merit)指標,特別針對非常數振幅的數位調變訊號經過非線性電路的影響有關。同時要注意,數位調變訊號的頻寬是頻譜分析儀(Spectrum Analyzer)的解析頻寬(Resolution Bandwidth, RBW)的好幾倍,因此量測時須使用頻段功率(Bandpower)的量測。
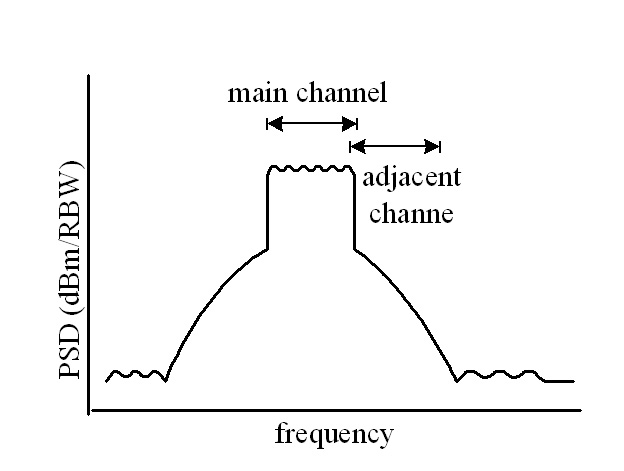 圖10 ACPR示意圖
圖10 ACPR示意圖
圖11是一個量測的例子,較新型的頻譜分析儀都會有頻段功率量測的功能,在左圖中主通道功率17.333dBm,右圖中主鄰近通道功率-8.319dBm,兩者相減得到ACPR=25.652dB。
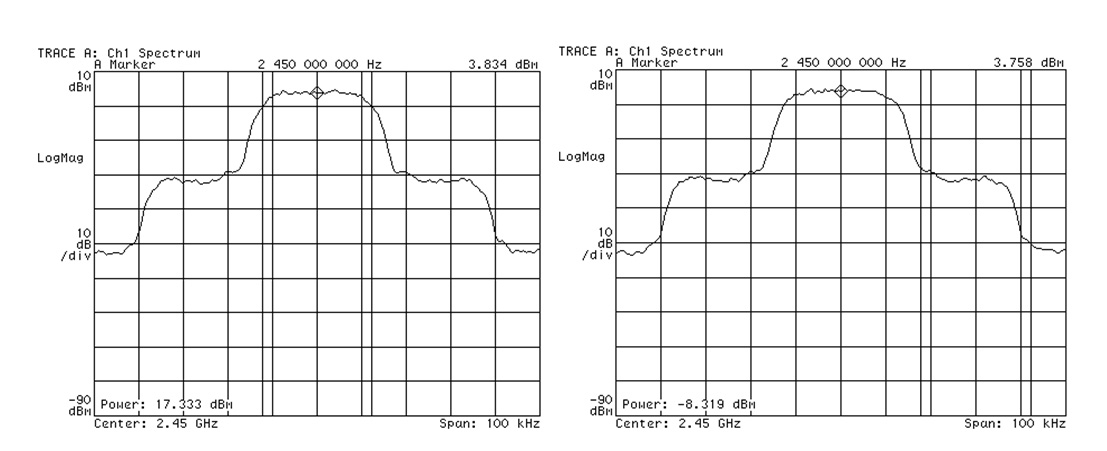 圖11 利用頻譜分析儀的頻段功率量測以計算ACPR示意圖
圖11 利用頻譜分析儀的頻段功率量測以計算ACPR示意圖
模擬結果與量測比較
考慮一個SRRC π/4-DQPSK的調變訊號,SRRC(Square-root Raised Cosine)表示根升餘弦訊號,接收端也會有一個SRRC濾波器,記住,因此同時達到零符號間干擾(zero ISI)及匹配濾波器(Matched Filter)的要求,以獲得在AWGN通道下有最佳的位元錯誤率(Bit Error Rate, BER)[5]。升餘弦濾波器之滾邊係數(Roll-off Factor) α範圍在0~1之間,α=0.35時之脈衝響應如圖12所示。為了達到zero ISI的結果,付出的代價就是調變訊號的振幅不是常數,因此經過放大器輸出之訊號品質容易劣化,這是放大器的非線性效應造成,透過撰寫模擬程式,可以深入了解這些現象。
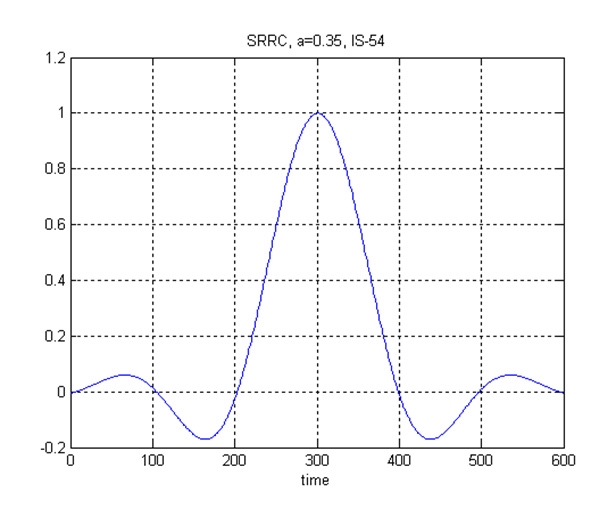 圖12 RC濾波器在α=0.35下之脈衝響應
圖12 RC濾波器在α=0.35下之脈衝響應
π/4-DQPSK是一種變形的QPSK調變,其做法是利用兩個位元的資料來決定下一個載波的相位變化,可能是±45o或±135o,形成一種交錯的QPSK調變,未經整形的π/4-DQPSK調變訊號的星座圖(Constellation Diagram)及相量圖(Vector Diagram)如圖13所示,黑色圓圈代表星星,即星座圖,也是訊號的取樣點。其間的連線代表訊號的路徑,由於它的路徑不會經過原點,因此經過放大濾波後失真會小於傳統的QPSK訊號。
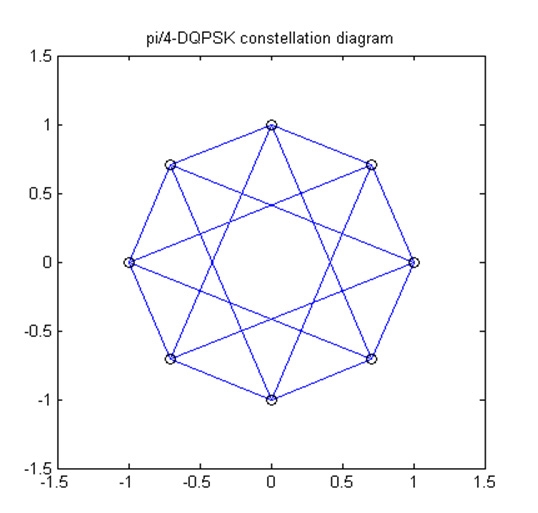 圖13 π/4-QPSK調變的相量圖
圖13 π/4-QPSK調變的相量圖
α=0.35的RC π/4-DQPSK調變訊號的星座圖加向量圖如圖14所示,圖中路徑與原點的距離代表瞬間振幅,可以看到瞬間振幅的變化。圖15為程式模擬之調變訊號的時間波形。由此圖可以知道在短時間內,訊號的波封(Envelope)變化相當劇烈,且最高的峰值與平均值相差很大。
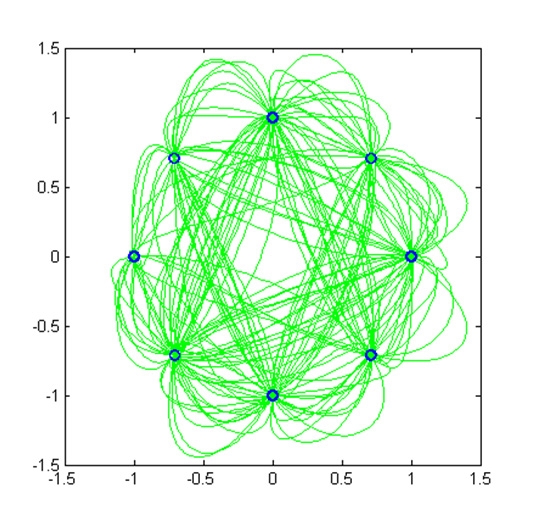 圖14 α=0.35的RC π/4-QPSK向量圖
圖14 α=0.35的RC π/4-QPSK向量圖
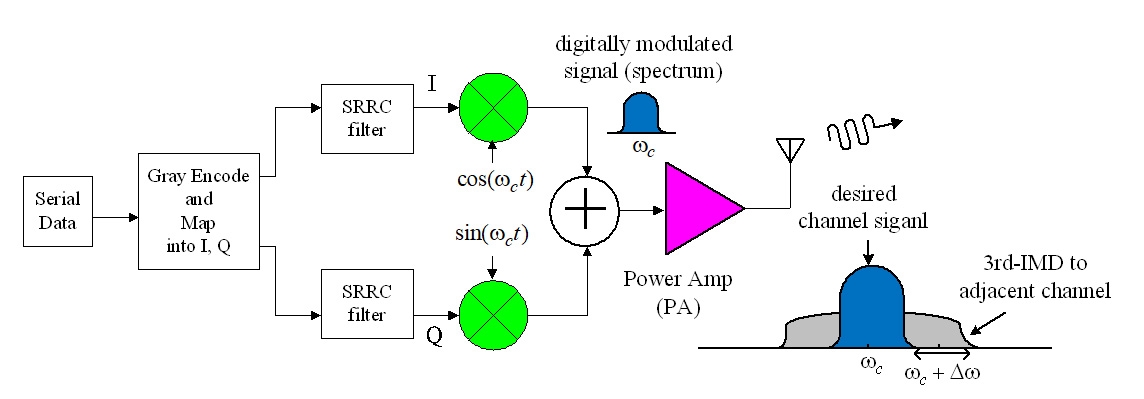 圖15 SRRC π/4-QPSK調變的時間波形
圖15 SRRC π/4-QPSK調變的時間波形
圖16是SRRC π/4-DQPSK的調變訊號產生並進入放大器的示意圖,其中在IQ調變前採用格雷編碼(Gray Coding)以降低一個符號錯導致兩個位元皆錯的可能性。
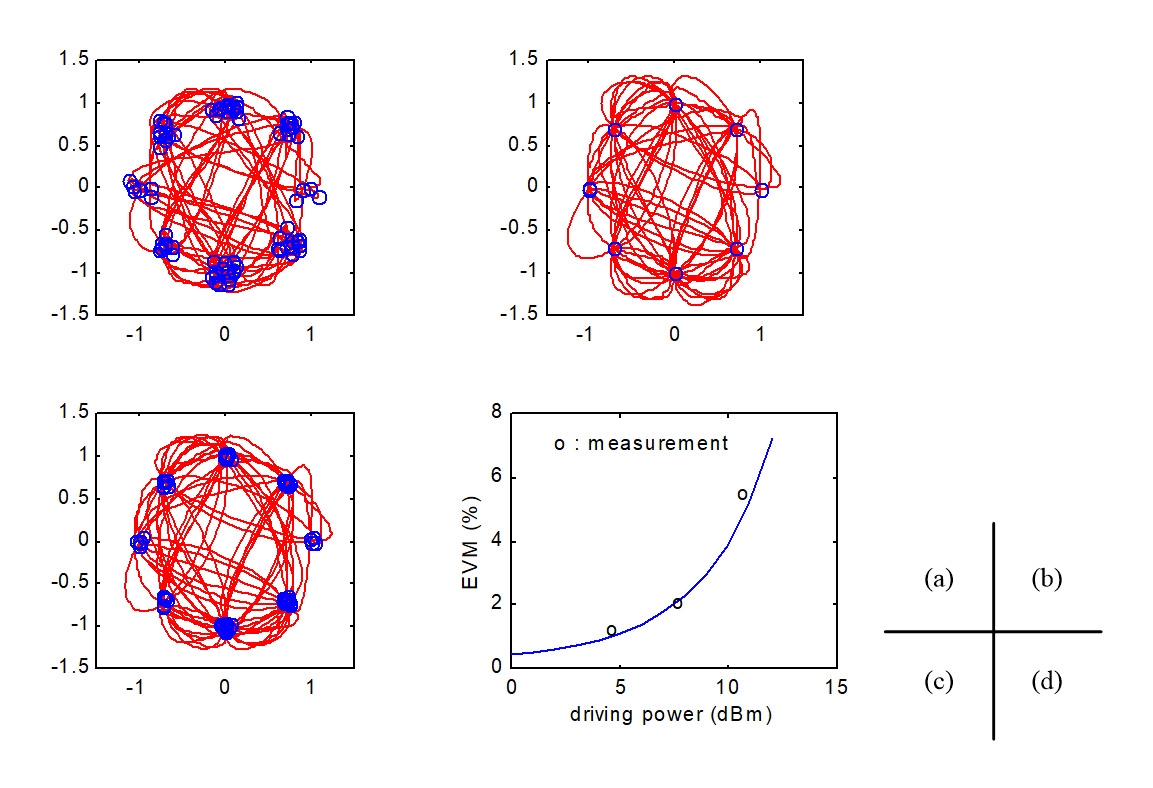 圖16 使用格雷編碼的SRRC π/4-DQPSK調變及放大示意圖[4]
圖16 使用格雷編碼的SRRC π/4-DQPSK調變及放大示意圖[4]
除此之外,模擬與量測的其他參數敘述如下:
G(2.4GHz MMIC PA的功率增益)= 11.5dB
OIP3=28.5dBm
Rs(符號傳輸速率)=24.5K symbol/sec
α(RC的滾邊係數)=0.35
NTRU(SRRC脈衝響應波形斷取符號(Truncated Symbols)的長度=8
BWmain(主通道頻寬)=33KHz
BWadj(鄰近通道頻寬)=33KHz
fadj(鄰近通道中心頻率)=fc+30KHz
EVM的模擬與量測的結果如圖17所示,注意到圖17(a)是發射端10.5dBm的SRRC訊號,還不是zero ISI,所以星座圖會明顯地散開。當訊號進入接收機或進入向量訊號分析儀,理想上經由接收或VSA內部另一個SRRC濾波器即可達到zero ISI的結果,如果還有向量誤差,就可確定是功率放大器(PA)的IP3造成的誤差。由圖17(d)可以看到模擬結果與量測相符。
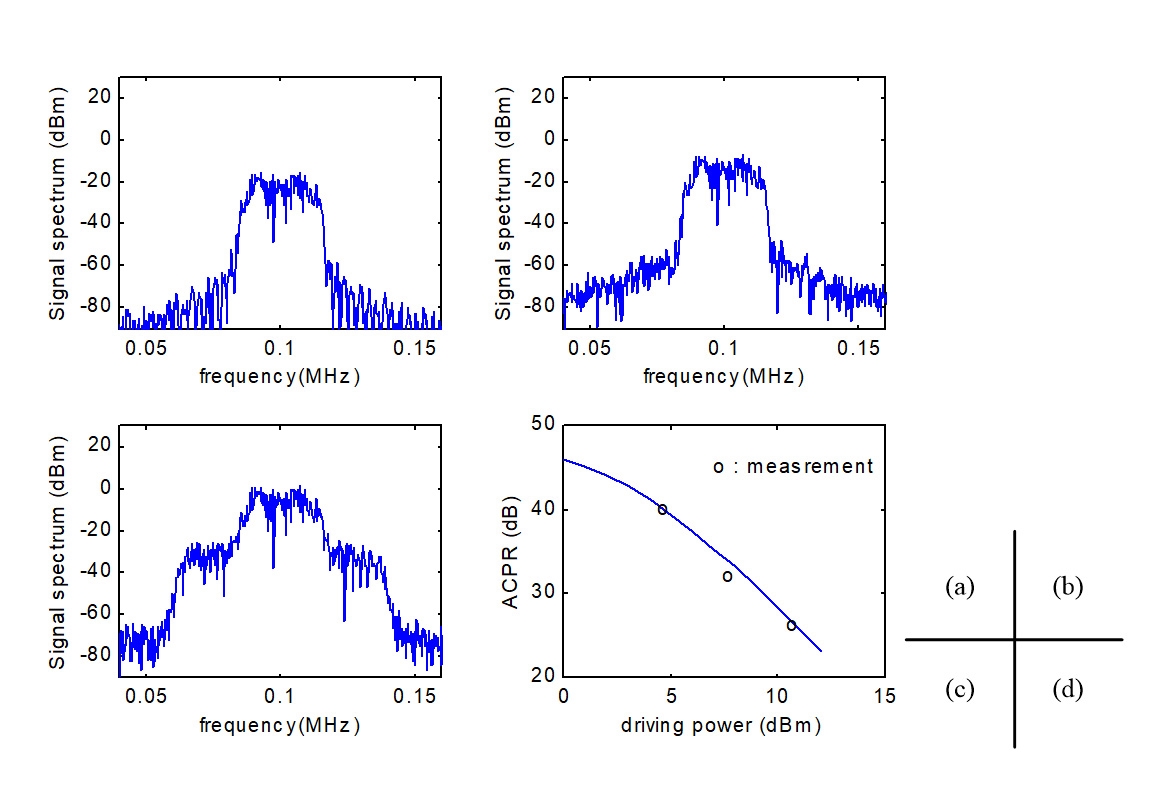 圖17 2.4GHz PA之EVM的模擬與量測:(a)模擬的10.5dBm輸入訊號的星座圖及向量圖,(b)當參考用的理想RC π/4-DQPSK的調變訊號,(c) PA輸出再經SRRC濾波器的結果,(d)程式預測與實際量測的比較
圖17 2.4GHz PA之EVM的模擬與量測:(a)模擬的10.5dBm輸入訊號的星座圖及向量圖,(b)當參考用的理想RC π/4-DQPSK的調變訊號,(c) PA輸出再經SRRC濾波器的結果,(d)程式預測與實際量測的比較
ACPR的模擬與量測的結果如圖18所示,之前的討論,此PA的輸入1dB壓縮點約為P1dB,in=PIOP3-(G-1)-9.6=28.5-(11.5-1)-9.6=10.4dBm,圖18(b)對應到輸入0dBm訊號的結果,由於0dBm離1dB壓縮點還有段距離,因此頻譜再生現象並不明顯。圖18(c)對應到輸入10.5dBm訊號的結果,已經超過1dB壓縮點0.1dB,所以可以很清楚地看到頻譜再生的現象,同時也降低了ACPR。如圖18(d)看到的,模擬結果與量測相符。
 圖18 2.4GHz PA之ACPR的模擬與量測:(a)模擬輸入0dBm訊號的功率頻譜,(b)模擬輸入0dBm訊號經PA放大的輸出功率頻譜,(c)模擬輸入10.5dBm訊號經PA放大的輸出功率頻譜,(d) ACPR的程式預測與實際量測的比較
圖18 2.4GHz PA之ACPR的模擬與量測:(a)模擬輸入0dBm訊號的功率頻譜,(b)模擬輸入0dBm訊號經PA放大的輸出功率頻譜,(c)模擬輸入10.5dBm訊號經PA放大的輸出功率頻譜,(d) ACPR的程式預測與實際量測的比較
基於改善EVM與ACPR的劣化,針對非常數振幅的數位調變訊號,將功率放大器的輸入功率回退(Backoff),可以避免過大的振幅峰值訊號進入放大器的飽和區,特別是OFDM調變訊號。以OFDM訊號為例,要精確地預測功率放大器輸入訊號的回退大小是不容易的,一方面不能犧牲功率放大器的功率效率(Power Efficiency),另一方面又要減低交互調變失真對鄰近子載波的干擾,這是另一個主題所要關心的。
使用Builder工具箱進行模擬
Builder工具箱大約是20年前的作品,它的前身是作者撰寫的MATLAB模擬軟體,可用來預測或計算串接射頻電路的整體參數。第一步先複製檔案Builder,第二步則點選Builder\runtime\setup,依指示完成安裝設定程序。而第三步驟為點選Builder\dedigit,或傳送到桌面建立捷徑,進入「頻譜訊號動態分析研究」,從螢幕按下即可得到圖19的結果。
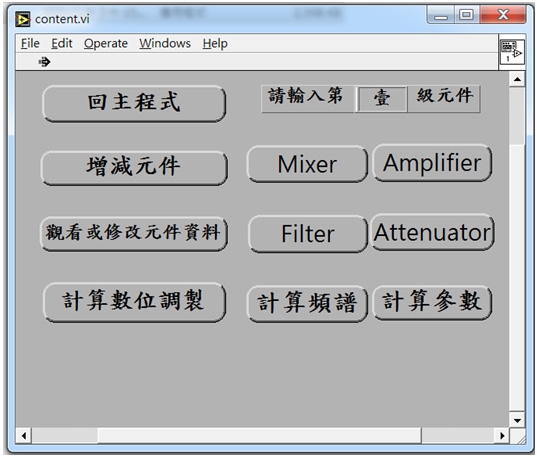 圖19 Builder工具箱套裝模擬軟體視窗
圖19 Builder工具箱套裝模擬軟體視窗
以Two-tone Test為例,一開始,先點選〔Amplifier〕,輸入增益改成10(dB),OIP3改成20(dBm),然後再點選〔OK〕按鈕(圖20)。接著點選〔計算頻譜〕,如圖21所示。隨後,輸入頻率解析度100,000Hz,輸入訊號頻率900(MHz),訊號功率-20dBm,再增加一組940(MHz),訊號功率-20dBm,點選〔OK〕,如圖22所示。
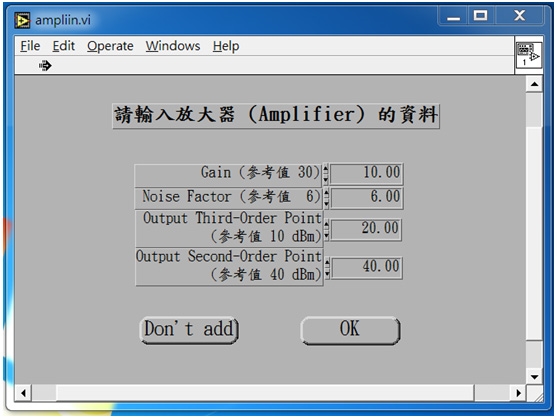 圖20 將輸入增益改成10(dB),而OIP3改成20(dBm)
圖20 將輸入增益改成10(dB),而OIP3改成20(dBm)
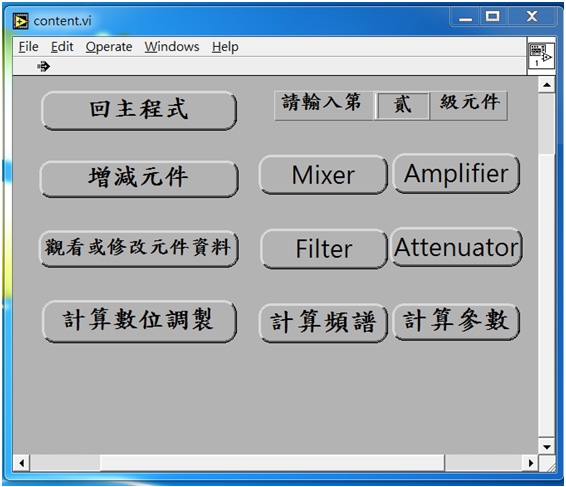 圖21 點選〔計算頻譜〕後的畫面
圖21 點選〔計算頻譜〕後的畫面
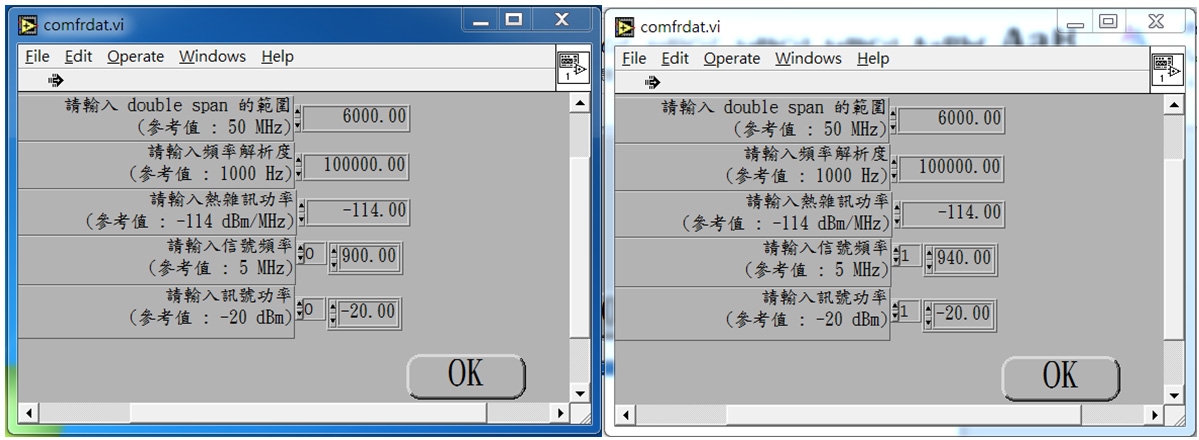 圖22 輸入頻率解析度、訊號頻率以及訊號功率
圖22 輸入頻率解析度、訊號頻率以及訊號功率
此時,觀看第0級表示輸入頻譜,觀看第1級表示放大器輸出頻譜。由輸出的十二種不同頻率及對應的不同功率的弦波訊號,可以看到Builder頻譜分析功能雙頻測試的結果(圖23)。
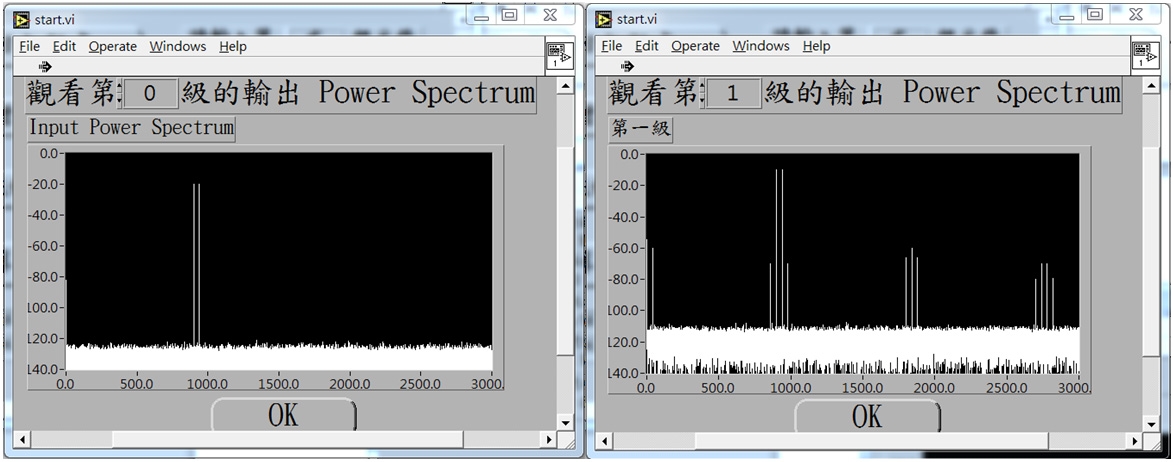 圖23 Builder的頻譜分析功能雙頻測試結果
圖23 Builder的頻譜分析功能雙頻測試結果
此外,還可以改變y軸與x軸的最大或最小刻度,以獲得適合觀看的頻譜。
串接元件的IP3
通常功率放大器的前級會使用驅動放大器(Driver Amplifier),兩級串接其等效的IP3為何?
與串接元件的雜訊指數(Noise Figure, NF)相比,由於每一級的雜訊都是不相關的(Uncorrelated),其造成的結果可以直接做功率相加,統計結果的運算簡單且明確。
IP3串接的問題則困難得多,比較可行的方法當然是做複雜的模擬或直接量測,因為兩級之間的頻率選擇電路也會影響整體的IP3結果。 考慮一個兩級串接的系統(圖24),其交互調變項(Itermodulation Poducts)是有相關性的,因此其加成是電壓相加,結果會跟各個別項的相位有關。
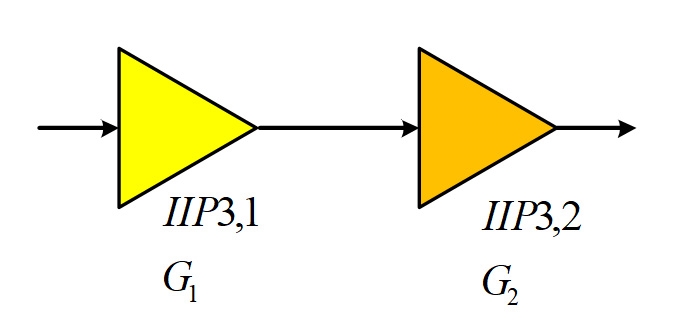 圖24 兩級放大器串接求IIP3的示意圖
圖24 兩級放大器串接求IIP3的示意圖
假設兩級的增益及輸入IP3以線性單位表示分別是g1=10G1/10、g2=10G2/10、p1=10PIIP3.1/10及p2=10PIIP3.2/10,再假設兩級之間只有頻率2f1−f2、2f2−f1、f1及f2的訊號通過,並考慮最差的狀況,經由數學推導及忽略不重要的其他項,可以得到兩級的輸入IP3如公式9所示[2]:
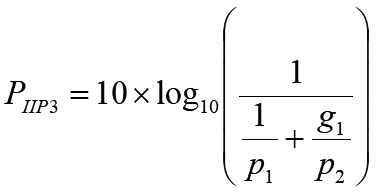
....................公式9
舉個數字的例子,G1=10dB即g1=10、G2=10dB即g2=10、PIIP3,1=20dBm即p1=100mW及PIIP3,2=30dBm即p2=1000mW,代入計算得到如公式10所示。
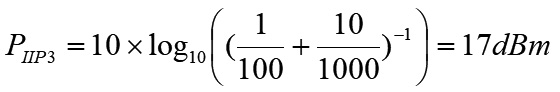
....................公式10
通常只要增益大於1,串接的IP3一定會小於各級最小的IP3。
