目前有許多種立體匹配技術被應用於解決在兩個影像之間尋找匹配點的問題。表1列出了常見的立體匹配技術和它們的優缺點。本文將介紹源自動態規劃(Dynamic Programming)概念的立體匹配技術,以及與此技術結合能降低運算成本的方法。
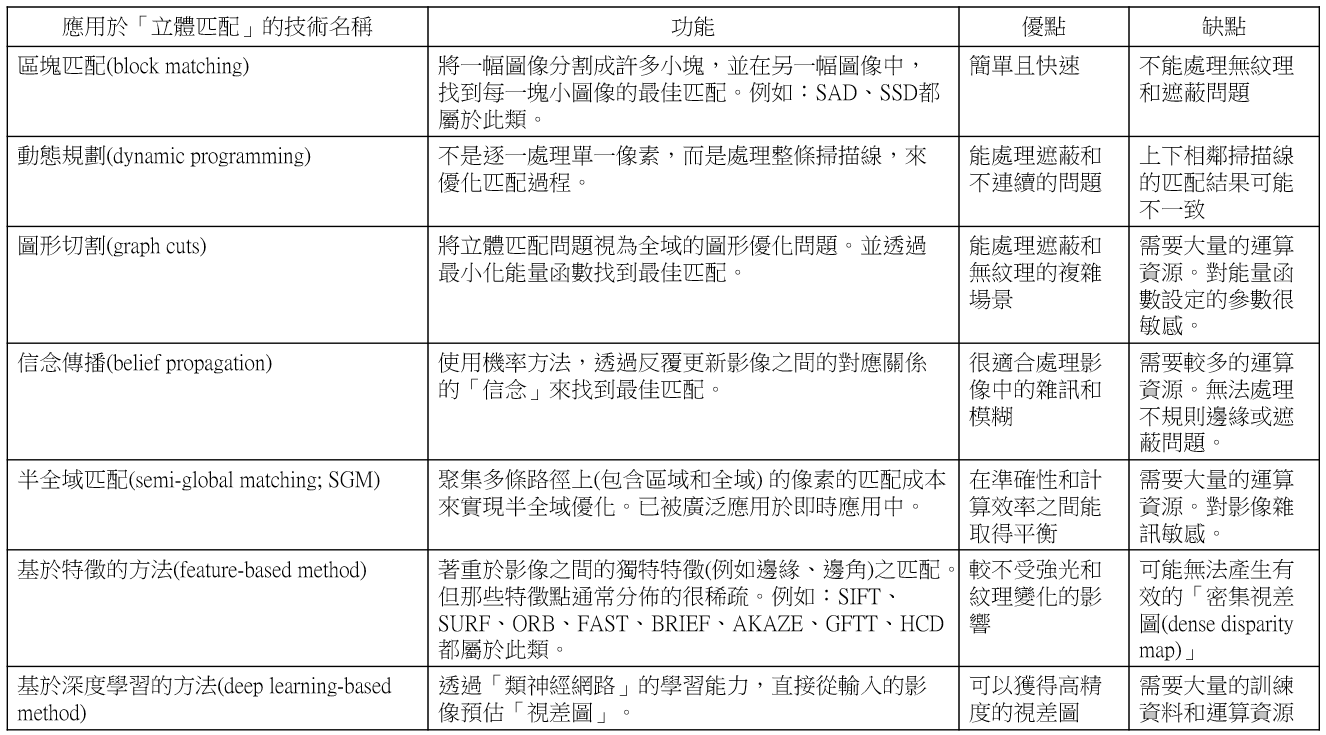 表1 應用於立體匹配的技術種類和優缺點之比較
表1 應用於立體匹配的技術種類和優缺點之比較
動態規劃
動態規劃是一種通用的演算法設計概念,最早由Richard Bellman在1950年代提出,用於解決具有重疊的子問題(Overlapping Subproblem)和最優的子結構性質(Optimal Substructure Property)的問題。在動態規劃中,如果可以從一個問題的子問題的最佳解中產出該問題的最佳解,則該問題具有最優的子結構;如果在計算過程中重複求解相同的子問題,則該問題具有重疊的子問題。
Needleman-Wunsch演算法是一種基因序列比對演算法,旨在找到兩個基因序列的全域最佳比對。它利用動態規劃的概念,透過構建評分矩陣(Scoring Matrix)和回溯矩陣(Backtrack Matrix)來找到最佳比對方案。這種方法的核心是最小化或最大化某種評分函數,並且在比對過程中逐步解決子問題,最終得到全域解。圖1是使用Needleman-Wunsch演算法求出評分矩陣的實例。
 圖1 使用Needleman-Wunsch演算法求出評分矩陣的實例
圖1 使用Needleman-Wunsch演算法求出評分矩陣的實例
圖2是雙目相機進行立體匹配時所採用的評分矩陣演算法,它是源自Needleman-Wunsch演算法。圖3是舉一個大小為4×5的評分矩陣E來說明。E是由輸入的序列(Sequence)l和序列2構成的,且序列1和2分別代表從雙目相機輸出的影像經水平對正(Rectification)後的掃描線。為方便說明,序列l的內容設為5634,序列2的內容設為57135,可將它們視為像素值(Pixel Value)。預先決定的評分規則分別是:單一間隔(Gap)是-1分,連續間隔(Extended Gap, Egap)是-1分,匹配(Match)是2分,如圖3(a)。不過,連續間隔的扣分通常低於單一間隔的扣分,這是為了鼓勵間隔能聚集在一起,而不是分散。
 圖2 立體匹配的評分矩陣演算法
圖2 立體匹配的評分矩陣演算法
 圖3 立體匹配的評分矩陣實例:(a)評分規則
圖3 立體匹配的評分矩陣實例:(a)評分規則
 圖3 立體匹配的評分矩陣實例:(b)最後完成的評分矩陣和選擇的最佳路徑
圖3 立體匹配的評分矩陣實例:(b)最後完成的評分矩陣和選擇的最佳路徑
 圖3 立體匹配的評分矩陣實例:(c)雙影
圖3 立體匹配的評分矩陣實例:(c)雙影
像序列對齊的結果
 圖3 立體匹配的評分矩陣實例:(d)兩條灰階的水平掃描線的視差演算法
圖3 立體匹配的評分矩陣實例:(d)兩條灰階的水平掃描線的視差演算法
所謂間隔或空位是因遮蔽(Occlusion)或無紋理(Textureless)造成兩個立體視覺影像不相符的區域。根據圖2立體匹配的評分矩陣演算法,可以求出E的所有元素值,如圖3(b)。最終的最佳對齊方式,可以從E的最後一行或最後一列且是最高分數的元素,沿著對角線回溯找到,如圖3(b)和(c)。在圖3(c)中,為了讓序列1和2的長度一致和能夠匹配,使用「-」表示間隔或空位。圖3(d)是根據圖3(c)的回溯結果,利用灰階像素的光強度,計算出視差映射陣列(Disparity Mapping Array),然後算出視差值陣列(Disparity Values Array)。
如此處理至累積成一個視訊訊框(Video Frame),就可輸出一個視差圖(Disparity Map)。式子(1)是E的第一行和第一列元素的初始值的計算步驟。E[0,0]是E的初始化位置,其初始值永遠為0,因為它代表比對流程的起點,不代表任何間隔或對齊的扣分,僅代表原點。式子(2)和(3)是分別求出E[1,1]和E[4,5]之值的計算步驟。不匹配(Mismatch)的扣分值是等於-ABS(l[i]-r[j]),ABS()是表示求絕對值。對角線(Diagonal)值=E[i-1,j-1]+match+mismatch;這裡的match是設為固定值2。
圖4是評分矩陣的資料流模型,可將它視為圖2的流程圖。在此評分矩陣的建構模組中,xy是代表圖2中的第i行和第j列,n、w、d分別代表:北方、西方、對角線的分數,比較這三個方向的分數,並選擇和儲存其中最高分者,同時將最高分者的方向儲存於Dxy。在回溯模組中,是利用評分矩陣重建路徑,或找到解決方案。回溯通常是從評分矩陣的最右下角具最高分的Eww元素開始,沿著對角線向上找出最高分的元素。
 圖4 評分矩陣演算法的資料流模型(包含建構模組和回溯模組)
圖4 評分矩陣演算法的資料流模型(包含建構模組和回溯模組)
圖4中的|x-y|等於圖2中的ABS(l[i]-r[j])。回溯可說是建構評分矩陣的逆向作業,所以x或y會根據Dxy儲存的方向遞減。如果Dxy儲存的方向是北方,則x減一行,向上走一格;如果Dxy等於西方,則y減一列,向左走一格;如果Dxy等於對角線,則x、y各減1,沿對角線往前走一格。如此回溯直到原點為止,最後得出圖2(c)的比對或匹配結果。

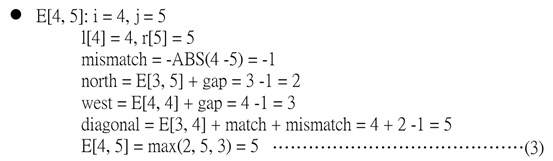
平行運算
若將全域比對減少為掃描線比對,則在給定的時間內,只需要考慮一條掃描線。並且,當一次僅處理一條掃描線時,所需的記憶體大小和運算複雜度會明顯少於一次處理整個影像。這對於運算資源很有限的嵌入式裝置而言,是很重要的。若想將評分矩陣演算法安裝到嵌入式裝置的主機板中,必須考量的重要因素有二:處理器的最高速率、可用的記憶體大小。通常需要採用一些編碼優化技術來克服這兩大限制因素,這些技術可區分為兩類:一是處理最佳化,旨在減少整體的處理時間;另一是記憶體最佳化,其目的是為了減少執行演算法所需的記憶體總量。
處理最佳化所採用的方法包括平行運算(Parallel Computation)、函數堆疊管理(Function Stack Management)和簡化循環週期(Loop Cycles)。此外,為了提高運算效率,還須盡量將演算法內的乘法運算改成加法運算,以及盡量使用暫存器或緩衝器來儲存變數,避免直接存取記憶體。由於立體影像的掃描線是彼此獨立的,因此雙目相機的影像解析度w×h(是以像素(Pixel)為單位),可分成h個連續的掃描線,在N個不同的處理器{P1,P2,...,Pn}中被執行,如圖5所示。
 圖5 四核心處理器的立體影像處理管道(Pipeline)
圖5 四核心處理器的立體影像處理管道(Pipeline)
此外,為了達到工作負載能平均分配於{P1,P2,...,Pn}處理器的目標,首先使用式子(4)來計算α參數,mod是取模數(Modulus),亦即h除以N的餘數。前α個處理器需負責處理L_α條掃描線,如式子(5)。其餘處理器需負責處理L_N-α條掃描線,如式子(6)。例如:雙目相機輸出的影像解析度是1920×1080,使用7個處理器,α=1080 mod 7=2,這表示前兩個處理器P1、P2需處理的負載各為L_α=[1080/7]+1=155。其餘5個處理器只需處理基本負載L_N-α=1080/7=154。掃描線的總數依然等於154×5+155×2=1080。

每條掃描線所需的處理時間,可能因為這三種因素而不同:(1)輸入影像的顏色分佈,分析某些區塊的複雜色彩需較多時間。(2)評分矩陣的計算,取決於視差(Disparity)。(3)回溯步驟。
理論上,動態分配能根據目前處理器的負載,即時指派每條掃描線l_left_h(t)和l_right_h(t)到特定的處理器P_n,達到平均分配工作負載、提高效率的目標。但實務上,如果事先不知道輸入的數據內容,則很難預測所需的處理時間。動態分配還會帶來額外的工作量,這包含徹底評估目前輸入的左右圖像中的掃描線、比較兩者的色彩分布、可能影響視差計算的圖案或紋理,以及可能影響立體匹配所需時間的其它因素。
這些都需要額外的時間和運算資源,特別是對於每行有許多像素的寬影像,因為處理時間與圖像的寬度成正比。所以,對於訴求低成本的3D雙目相機裝置而言,使用即時動態分配的效益並不如使用式子(4)至(6)的方法,因為它很簡單,又能預先確定各處理器的工作負載,易於實作。而且,它還能確保資源的有效利用,並可減少因立體匹配所產生的時間延遲。
記憶體優化
為了評估所需的記憶體總量(以位元組為單位),定義下列參數和計算式,但不考慮演算法程式中微不足道的局部變數:
- 輸入一張圖像的解析度(w×h):亦即雙目相機的影像解析度,以像素為單位。
- 輸入圖像的通道數量c:若c=3代表RGB圖像;c=1代表8位元的灰階(Grayscale)圖像。
- 能表示評分矩陣的元素(ei,j)最大值的位元組ε:i,j分別是評分矩陣的行數和列數。此處的評分矩陣是正方矩陣(Square Matrix)。因為輸入的是兩圖像的水平掃描線,i,j之值是介於1和w之間,而且i和j的最大值都等於w。如圖6所示。
- 從左相機輸入的圖像大小(w×h×c位元組)
- 從右相機輸入的圖像大小(w×h×c位元組)
- 輸出灰階的視差圖大小(w×h位元組)
- 評分矩陣的大小(N×w×w×ε位元組)
 圖6 計算評分矩陣的元素最大值
圖6 計算評分矩陣的元素最大值
演算法剛開始被執行時,若只用到一個處理器,評分矩陣E所分配到的記憶體區域是可重覆使用的。此時,單一處理器會依序計算輸入的每對掃描線的每個像素的得分,若舊的得分值不需要時,則新的得分值會覆蓋掉其記憶體位址的內容。但當輸入的掃描線數量增加時,會使用到N個處理器,此時每個處理器核心都必須擁有各自專用的記憶體區域。
因輸入至評分矩陣的每個像素值的最大值和單一間隔、連續間隔的最大設定值、對角線匹配的最大設定值都是255,而且當兩序列相同時,在對角線上的元素值是累加的,這時在評分矩陣的最右下角可得到最大元素(ew,w)值w×255。在評分矩陣的每個元素值,都包含兩個部份:得分、方向。使用21個位元足以表示得分部份,方向是用3個位元表示。所以ε等於3位元組,亦即24位元,如圖7。將輸入的兩圖像大小、輸出灰階的視差圖大小、評分矩陣的大小加總,於是需要的記憶體總量M可由式子(7)得出。
 圖7 一個24位元的評分矩陣元素ei,j和32位元的記憶體位址對齊
圖7 一個24位元的評分矩陣元素ei,j和32位元的記憶體位址對齊
因為在計算元素ei,j之值時,需使用(i–1,j)、(i–1,j–1)和(i,j–1)三個元素之值,但其實這只需要評分矩陣中的i和(i–1)這兩行即可,不需要整個評分矩陣,因此所需的評分矩陣大小可以從w×w×ε減少至2×w×ε(位元組)。此外,在進行回溯時,可能需要不同的方向或額外資訊,所以每個像素還需要額外的4個位元,因此需要的額外記憶體大小是4×w×w(位元)或w×w/2(位元組),由此導出的記憶體總量如式子(8)所示。而式子(9)與式子(8)相比,它的h等於1,這表示它除了逐行計算輸入的一對掃描線以外,輸出也是一條掃描線或立體線(Stereo Line)。這種優化方法被稱作行版本(Line Version),也是使用記憶體總量最少的版本。
