在行動通訊的領域,以發射端為例,波束成形(Beamforming)通常是利用訊號處理的技術結合多根天線產生一個具有指向性的波束,將波束集中在希望傳播的方向,可以提升該方向訊號的能量並減少對其他方向用戶的干擾。
簡易的波束成形的運作是利用波束成形控制器控制每一根天線的輻射訊號的相位,使得多個輻射訊號在某些方向波幅相長干涉,在另一些方向則形成相消干涉。波束成形也可以使用在接收端,針對不同接收天線收到的訊號給予適當的相位控制再相加,可以增強來自於某方向的電波訊號,並抑制另一些方向的訊號。
認識天線陣列
天線是無線通訊的重要設備,它可以釋放電磁能量至自由空間(Free Space),也可以從空中接收射頻能量。
天線教科書裡有一個理論叫做互易定理(Reciprocity Theorem),此定理說明一根天線無論是作為發射還是接收,它的方向場型(Directional Pattern)是完全一樣的[1]。當然,真實世界會有其他的考量,例如調幅(AM)廣播的發射天線是75公尺(m)的巨型鐵塔,但收音機的接收天線卻簡單繞幾個金屬迴路即可。本文在往下的討論,不論發射還是接收,天線本體及其場型對發射或接收來說都是一樣的。
將多根性能相同的天線在空間適當的擺放,例如直線形、半圓形、正三角形等等,稱之為天線陣列(Antenna Array),再配合適當的控制訊號的振幅與相位,即可控制輻射場型的各項參數,例如主波束(Main Beam)的方向、波束寬度(Beam Width)與方向增益(Directivity)、旁波束的準位(Sidelobe Level)等等。
天線陣列產生的場型函數(Pattern Function)通常由兩個因數決定[1],一個稱作元件因子(Element Factor),另一個稱作陣列因子(Array Factor)。元件因子是單一天線的輻射場型(Radiation Pattern),陣列因子則跟兩個因素有關,一是陣列的幾何排列形狀,另一是對應個別天線訊號的權重(Weight),包括振幅及相位的改變。
場型乘積定理(Principle of Pattern Multiplication)說明,相同天線構成的陣列,其場型函數等同於元件因子與陣列因子的乘積。如果元件因子是一個常數函數,則場型函數與陣列因數相似,只差了一個比例常數,本文以下的解說都是這樣的例子。
另外,考慮真實的情況,當兩根天線靠近,流經天線的電流會互相作用,產生所謂的互耦合效應(Mutual Coupling),會影響到輸入阻抗及輻射場型,本文先合理的假設互耦合效應可以忽略,避免更複雜的討論。
較常見的多天線組態是等間距直線排列的天線陣列,為了說明的方便性,底下以間距1/2波長(λ)的半波偶極(Half-wave Dipole)天線陣列來舉例,如圖1所示。
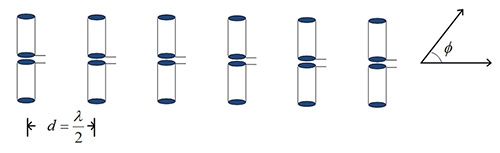 圖1 間隔1/2波長的半波偶極天線陣列示意圖
圖1 間隔1/2波長的半波偶極天線陣列示意圖
半波偶極天線是一種廣泛被使用的天線[2],原因包括:(1)其輻射場型在水平方向是全向性的(Omnidirection),元件因數是一個常數函數;(2)具有合理的方向增益(Directivity)約2.15dB(=1.64);(3)輸入阻抗(Input Impedance)約73歐姆(Ω),與50歐姆的無線通訊系統接近,即使不做匹配,電壓駐波比(VSWR)也不會很高。
垂直極化的半波偶極天線其遠場(Far-zone Field)的三維(3D)輻射場型像水平擺放的甜甜圈,如果沿著水平去看它,它是一個正圓,圖2是垂直極化的半波偶極天線在水平方向的輻射場型,如果沿著某一個縱軸觀看它,它就會像是圖3所看到的8字形。
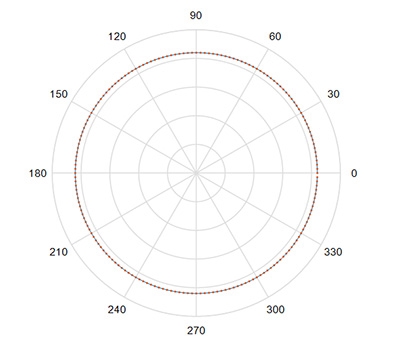 圖2 半波偶極天線在水平方向的輻射場型
圖2 半波偶極天線在水平方向的輻射場型
圖3與教科書上的形狀略有不同,這是因為本文所有的場型圖刻度單位都是以dB表示,而一般書上畫極座標圖習慣用線性單位。由於這裡關心的是地球表面的行動通訊,且天線陣列是水平的沿著假想的x軸擺放,因此從現在開始針對元件因子只須關心圖2的正圓場型即可。
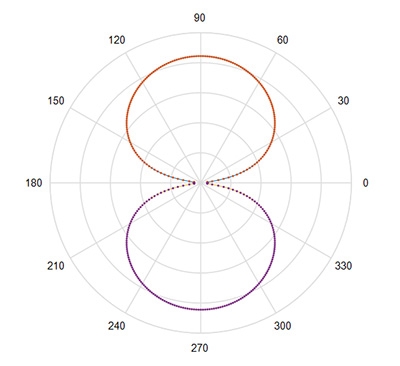 圖3 沿著某一個縱軸的輻射場型
圖3 沿著某一個縱軸的輻射場型
波束成形與天線間距
等間距的天線陣列其間隔通常設定為半波長,為了說明的方便性,這裡以Matlab撰寫程式跑一些天線陣列場型來說明這個重要的概念,採用的是最簡易的共軛空間複數特徵法[3],此法只改變訊號的相位,程式撰寫的原理討論留在文章後段再說明。
假設半波偶極天線的根數N=6,指向𝜙=60°,天線的間距分別是d=λ/4、d=λ/2、d=λ及d=3λ/2。圖4為不同間距的結果,只往前看,也就是說只看𝜙=0°到𝜙=180°的場型,即圖形的上半部。圖4(a)為間隔d=λ/4的結果,可以看到指向𝜙=60°的主波束太寬,也就是空間解析度不是很好。
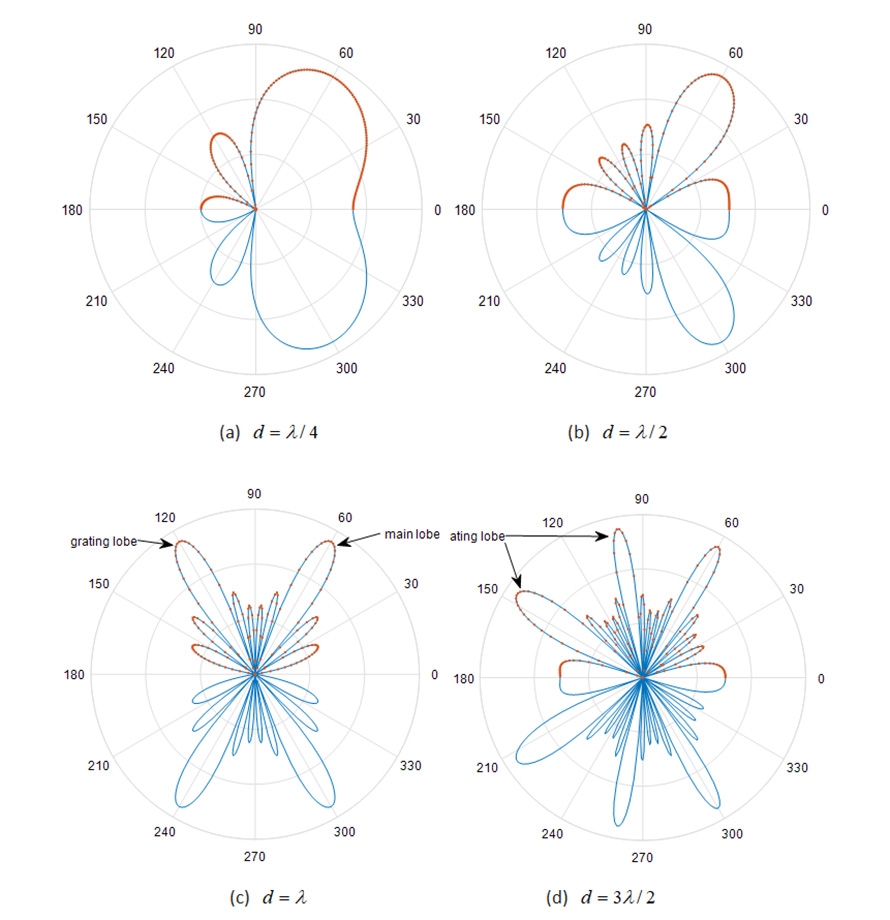 圖4 N=6的半波偶極天線陣列在水平方向的輻射場型:不同天線間距
圖4 N=6的半波偶極天線陣列在水平方向的輻射場型:不同天線間距
圖4(c)為間隔d=λ的結果,可以看到指向𝜙=60°的主波束很窄,空間解析度很好,但是會產生旁瓣輻射(Grating Lobe)的效應[2],這是不好的現象。以發射來說,幾乎浪費了一半的功率在𝜙=120°的地方,並造成在𝜙=120°附近的電波干擾現象。以接收來說,會產生空間混疊的現象,如圖4(c)所看到的,𝜙=0o到𝜙=90°的場型如鏡像般出現在𝜙=180°到𝜙=90°。這時候再回來看圖4(b),其間隔d=λ/2,沒有旁瓣輻射(Grating Lobe)的效應,空間解析度還算恰當,這也是大家選擇間隔d=λ/2的原因。
其實只要間距比d=λ/2大一些,旁瓣輻射的效應就會開始出現,到達d=λ則以完全對稱的方式出現,圖4(d)為間隔d=3λ/2的結果,可以看到更多的旁瓣輻射。電波源的入射方向估測(Direction Finding)是另一門利用陣列天線的學問,可以結合波束成型以達到智慧型天線(Smart Antenna)的要求,做方向估測時間距也都是d=λ/2[3],如此才能避免空間混疊的現象。
在某些領域,譬如太空探測,關心的可能是天空小範圍的區域,為了提高解析度,可以讓間距比d=λ/2大很多,以產生更大的孔徑(Aperature)。有一種陣列稱作稀疏陣列(Sparse Array),經由模擬及計算,可以得到較佳的稀疏幾何形狀(Geometries)陣列,在小範圍的追蹤角度(Steering Angle)可以獲得很好的峰值對旁波束比(Peak-to-sidelobe Ratio)。
何謂二項式陣列
為了趣味性,這裡暫時偏離主題。觀察圖4(b),可以看到N-2=4個較小幅度的旁波束,在某些應用裡,如果不希望旁波束出現,可以考慮採用二項式陣列(Binomial Array)[1]。
顧名思義,二項式陣列即是利用二項式係數當做個別天線訊號的振幅權重⎜W⎟=[1,5,10,10,5,1],以N=6為例,振幅權重,也可以說是巴斯卡(Pascal)三角形的第六列,假設𝜙=105°及𝜙=60°,程式跑出來的結果分別如圖5(a)及圖5(b)所示。
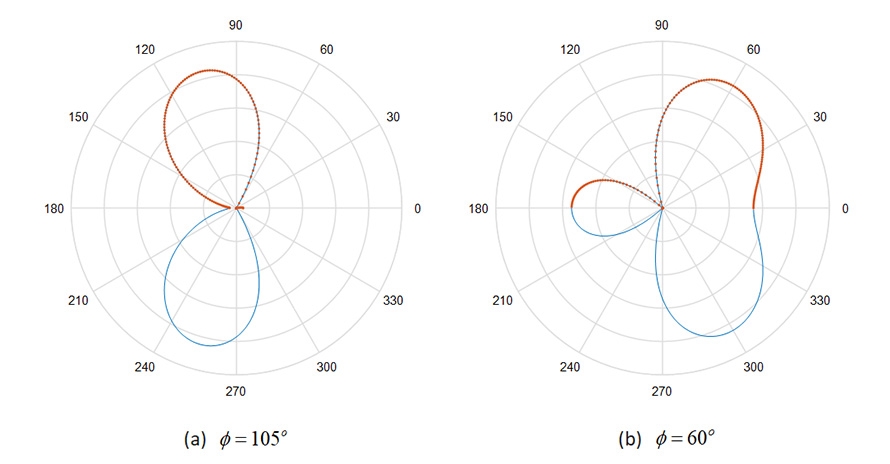 圖5 N=6的二項式陣列天線在水平方向的輻射場型
圖5 N=6的二項式陣列天線在水平方向的輻射場型
由圖5(a) 𝜙=105°的情況可以看到旁波束消失了,當然也付出了其他的代價,包括較寬的主波束及較低的方向增益,猜測原因是3號與4號天線振幅太大,主導了主波束的場型,等同於有效陣列長度只有N=2,其他四根天線的功能只是為了消除旁波束,因此在波束成形的領域,重點應該擺在相位的改變,振幅權重的變異盡量不要太大,或是說統計上的標準差(Standard Deviation)要盡量接近0,以提升這一類應用的性能。
改變各種∅的數值,當𝜙≥110°或𝜙≤70°,還是會有半個旁波束漸漸出現,例如𝜙=60°的情形如圖5(b)所示。
波束成形與方位角
再回到主題,一樣以N=6為例,這次換改變各種方位角∅的數值,𝜙=[0o,30°,60°,90°,120°,150°],結果如圖6所示,由圖中可以看出隨著不同的方位角設定,波束的最大幅度方向也會跟著改變,波束成型的效果在30°≤𝜙≤150°會比較好,此外也發現到在𝜙≤30°或𝜙≥150°,另一類的旁瓣輻射又出現了,觀察𝜙=0°的場型就可以看到在𝜙=180o出現明顯的旁瓣輻射。做個結論,直線排列的天線陣列架構較適合操作在30°≤𝜙≤150°的120°範圍內,若組成正三角形排列應該是不錯的選擇,要不然就考慮更複雜的半圓形架構。
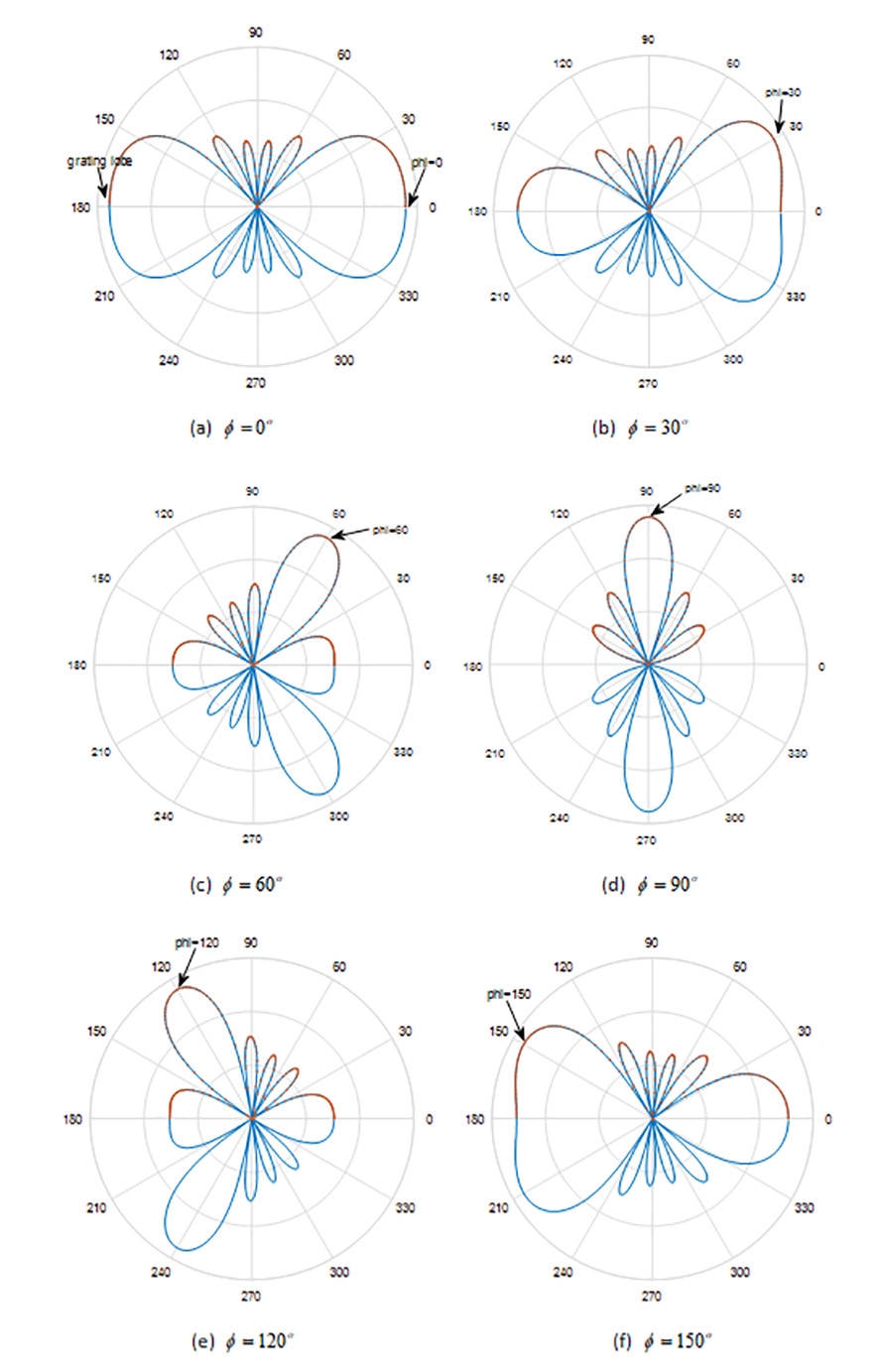 圖6 N=6的半波偶極天線陣列在水平方向的輻射場型:不同方位角
圖6 N=6的半波偶極天線陣列在水平方向的輻射場型:不同方位角
波束成形與陣列天線根數
接著,改變天線根數的數值N=[3,6,12]來觀察根數的影響,方位角指向𝜙=60°,結果如圖7所示,圖7(a)是N=3與N=6的比較,由圖中可以看出N=6的主波束比N=3窄,方向增益也比較大,同時旁波束的幅度也較低。圖7(b)是N=12與N=6的比較,由圖中可以看出N=12的主波束比N=6更窄,方向增益也更大。結論是天線根數越大,波束成型的效果越好,當然整個控制網路及計算也會變複雜。
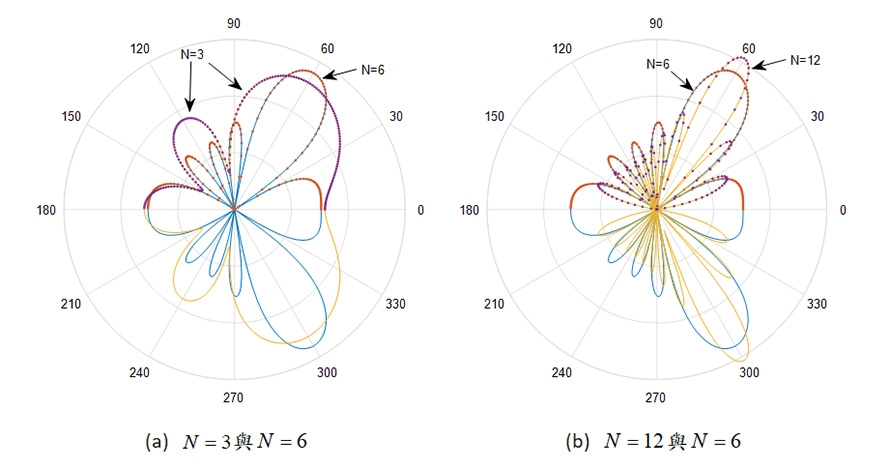 圖7 半波偶極天線陣列在水平方向的輻射場型:不同天線根數
圖7 半波偶極天線陣列在水平方向的輻射場型:不同天線根數
再仔細觀察圖7(b)的兩個主波束的峰值,大約相差3dB。下面試著針對發射和接收做不同的說明。考慮發射的情況,假設總功率一樣,天線根數變兩倍,每根天線分到的功率少一半,也就是減少3dB,但是朝著𝜙=60°輻射出去的方向,電場的振幅是直接相加變兩倍,所以功率變四倍,即6dB,6dB-3dB=3dB。
接著考慮接收的情況,天線根數變兩倍,沿著方向∅=60o經天線進來的電波,由合成器相加成為兩倍的電壓,所以接收功率變四倍,即6dB。對接收機來講,這裡關心的是訊號雜音比,由於每根天線進來的熱雜訊是不相關的高斯隨機程序(Gaussian Random Process),期望值為0,因此雜訊相加平均功率變兩倍,即3dB,6dB-3dB=3dB。結論是不管發射或接收,天線根數變兩倍,通訊性能就提升3dB。
LES天線陣列與波束成形原理
至此,再對前面提到的間距1/2波長(λ)的半波偶極天線陣列做深入的討論。每根天線元件以固定距離直線排列組成的陣列,稱為線性等距離陣列(Linear Equally Spaced Array, LES)天線。借用教科書[3]的內容,為了配合數學的說明,底下有些變數會稍與前面不同。
通常為了簡化天線陣列的分析,以接收端為例,都會假設以下條件:(1)陣列天線中天線元件之間的間隔距離夠小,使得每一根天線元件所收到的訊號振幅皆相同;(2)元件之間沒有互耦合的現象;(3)所有的入射場型可以被分解為有限的平面波(Plane Wave);(4)入射訊號的頻寬遠小於載波頻率。
圖8顯示了一組沿著x軸排列的LES及其合成網路(Combining Network),𝜙稱作入射電波的方位角(Azimuthal Angle),通常還會有另一個變數θ是入射電波的高度角(Elevation Angle),水平面被表示為θ=π/2,因此以下的討論不會出現變數θ。
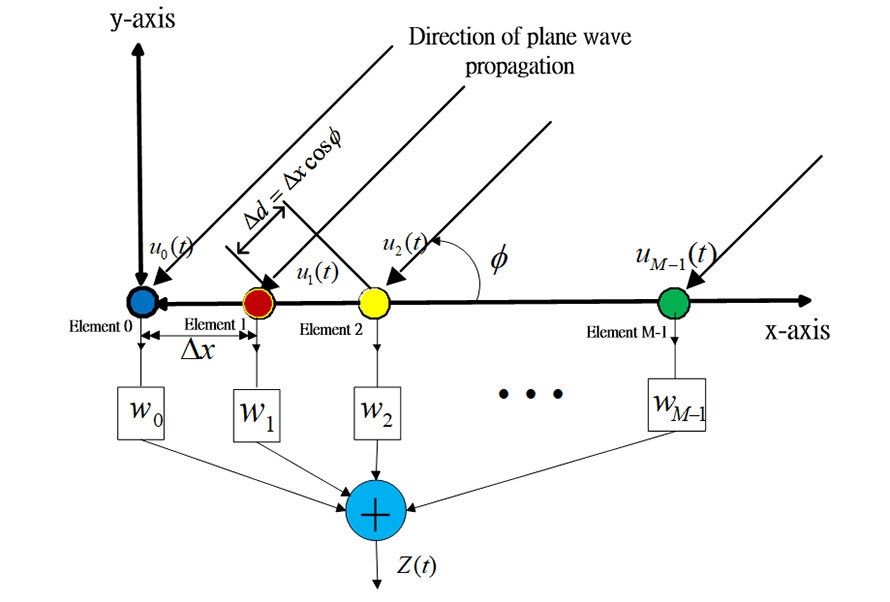 圖8 接收端天線陣列的基頻複數包跡模型
圖8 接收端天線陣列的基頻複數包跡模型
圖8的模型也稱作基頻複數包跡模型(Baseband Complex Envelope Model),雖然電波的中心頻率可能高達譬如79GHz,但是依然可以使用低頻等效(Lowpass Equivalent)的技巧來說明波束成形的原理。
假設通訊環境為地球表面,有一個平面波𝜙從方向入射到陣列,天線間距∆χ=λ/2,β=2π/λ稱為相位傳播係數(Phase Propagation Factor)。每根天線與參考點(最左邊的第零根天線元件)之間的相位差以追蹤向量(Steering Vector)表示,如公式1所示:
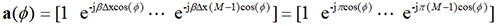
..............公式1
波束成形原理是藉由調整天線陣列加權的方式,使無線電波場型的主波束朝向期望的方向,以增強訊號強度和抑制其他方向的干擾。最簡單的波束合成法,一般給它一個名稱,叫做共軛空間複數特徵法,此法只控制訊號相位,不控制振幅。
假設使用者的入射角度已知或已被估測出來,令加權為追蹤向量的共軛並將方位角∅代入,如公式2所示。從數學觀念來看,若有一個複數向量與它的漢彌頓轉置(Hermitian Transpose)向量相乘會得到一個最大值,意味著此方法可以壓低其他角度的訊號,使所估出的入射角度有最大的疊加。漢彌頓轉置包含複數共軛(Complex Conjugation)及向量轉置,其中每一個權重如公式2:
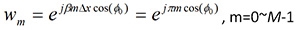
..............公式2
由於元件因子是一個常數,所以場型函數與陣列因子相似,只差了一個比例常數,場型函數可以表示為公式3,透過此式子可以繪出此天線陣列的輻射場型。
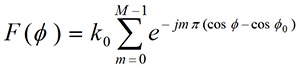
..............公式3
例如,假設入射角度𝜙°=30°已被估測出來,透過共軛空間複數特徵法可形成朝向∅o=30o的最大比例接收環境場型,如圖4(b)所示。
再回到圖8,如果把圖中所有路徑的箭頭皆反向,並將合成器改為分配器,則此模型即變成發射端的基頻複數包跡模式。以發射端為例,在基頻乘上ej30°,數學上也等同於在中頻(IF)或在射頻(RF)的高頻訊號移相30°,實作上如何決定是基頻、中頻還是射頻?這時就得考慮整體電路的複雜度、參數的精準度、控制的困難度、技術是否做得出來、成本花費等等。以5G毫米波為例,也許可以分成粗調及細調,由不同的基頻、中頻或射頻選兩者來分工完成。
智慧型天線淺談
粗略來說,智慧型天線是由一組天線元件,採特定幾何形式排列結合訊號處理技術所組成,透過適應性的(Adaptive)方式控制主動元件去改變無線電波幅射場型,具有提高通訊品質、增加系統容量的能力。雖然天線只有一組,但是透過陣列訊號處理就可以產生多組的場型,也稱作多波束智慧型天線,如圖9所示,圖中共有四種場型,分別可以接收來自四個方向的訊號,分別是𝜙=30°,60°,75°,120°。
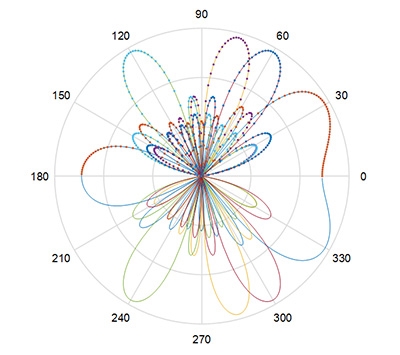 圖9 天線陣列指向四個不同方位角的的輻射場型
圖9 天線陣列指向四個不同方位角的的輻射場型
智慧型天線是利用天線陣列來取得訊號的空間特徵(Spatial Signature)差異,透過空間分隔多重存取(Spatial Division Multiple Access, SDMA)技術分離出所接收到的訊號,同時減少其他使用者的干擾和多重路徑造成訊號衰弱及符號間干擾(Intersymbol Interference, ISI)現象。單獨一根天線所能提供的自由度有限,因此在相同的發射功率之下,天線陣列可提升接收訊號的強度及系統性能增益,也可提供多樣的波束掃描、追蹤及零位消除(Nulling)等功能。
智慧型天線系統可產生空間定向波束,將其中主波束朝向所要接收用戶的方向,旁波束或零點(Null)對準干擾訊號的方向,以達到壓抑或濾除干擾訊號的目的,同時利用各用戶之間空間特徵的差異,透過陣列天線技術在同一通道上做接收或傳送多個用戶訊號,使頻譜的使用更有效率。
以行動通訊的接收來說明,考慮上鏈(Uplink)的情況,基地台的陣列天線接收到行動端所發射的訊號,由射頻/中頻接收單元轉換成基頻訊號,再使用DOA演算法估測各個使用者與其多重路徑之到達方向(Direction of Arrival, DOA),利用估測的DOA的資訊可經由波束合成的最佳化成演算法產生一組最佳化複數之加權向量,透過此加權向量與接收訊號結合運算將可加強期待者的訊號,抑制其他使用者與外來雜訊之干擾。
在下鏈(Downlink)時,基地台經由上鏈時所取出的DOA或是訊號空間特徵,經由上述最佳化波束成形演算法的處理後,經由射頻/中頻發射單元轉成高頻訊號傳送至行動端。基地台經由陣列天線將K個訊號同時發送給每個用戶端,為了減低其對其他用戶端所造成的干擾,智慧型天線系統針對每個用戶端設計其對應的加權向量,這也意味著智慧型天線系統可以同時為每個用戶端設計出最佳的接收環境,抑制其他使用者的干擾,將彼此訊號的相關性降到最低。
智慧型天線一般演算法分為盲式(Blind)和非盲式(Non-blind)兩大類(圖10)。盲式是直接將接收到的訊號經過數學運算,解出訊號入射角度,再透過波束成形技術。非盲式是在每次傳送訊號的過程中每隔一段時間就傳送一訓練序列(Training Sequence),利用訓練序列資料來得到某些最佳的情況,例如訊號對干擾及雜訊的功率比(Signal to Interference and Noise Ratio, SINR)。這裡各舉一個例子做簡要的說明,分別是圖中的MMSE及MUSIC。
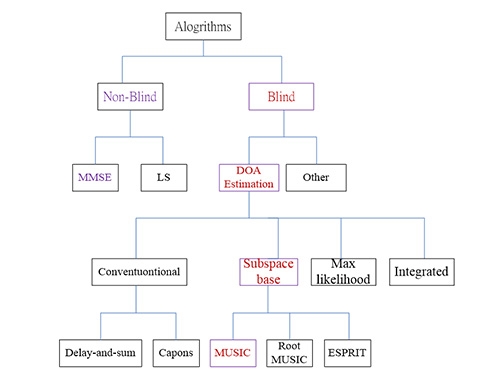 圖10 一般智慧型天線演算法分類
圖10 一般智慧型天線演算法分類
最小均方誤差(Minimum Mean Square Error, MMSE)方法是非盲式的,它並不需要DOA的演算法,但需要參考訊號作為陣列天線場型的調整,這個參考訊號稱為訓練序列。此法要求發射端在固定的時間間隔傳送正確的訓練序列做為加權向量的校正。
MMSE方法先定義代價函數(Cost Function),再求得代價函數的最小化,也就是希望藉著MMSE的方法得到接收訊號與其期待訊號的誤差最小,經過一系列的數學推導得到這個方法的第n位使用者的加權向量選擇為[3](公式4):
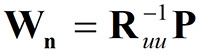
.............公式4
其中Ruu是資料向量的共變異數矩陣(Covariance Matrix),P是資料向量與第n位使用者期待訊號向量的交叉相關向量(Cross-correlation Vector)。
圖11說明了在陣列天線數目為8時,以MMSE方法模擬所得到的天線場型,可以看出使用者從三個方向40°、0°、20°而來,可以發現MMSE方法針對來自𝜙=40o的使用者形成一個主波束而抑制從𝜙=0°及𝜙=20°的使用者的干擾。圖中的SOI(Signal Of Interest)是接收端想要的訊號,SNOI(Signal Not of Interest)則是接收端不感興趣且極力想排除的訊號,此類的陣列訊號處理即是空間濾波器(Spatial Filter)的概念。
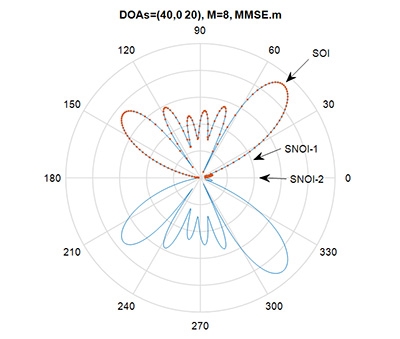 圖11 使用MMSE方法所求得之場型圖,SOI之DOA=40o,SNOI之DOA=20o及0o
圖11 使用MMSE方法所求得之場型圖,SOI之DOA=40o,SNOI之DOA=20o及0o
第二個例子屬於盲式,先做DOA估測,再使用譬如前面提到的共軛空間複數特徵法。DOA估測是利用訊號空間與時間的關係,透過計算找出空間中電波訊號來源的入射角度。
一般DOA估測技術分為四類[3],包括傳統技術(Conventional Techniques)、子空間基底技術(Subspace Based Techniques)、最大可能性技術(Maximum Likelihood Techniques)以及積分技術(Integrate Techniques),如圖10所示。
MUSIC(Multiple Signal Classification)是以子空間為基礎的演算法,由Schmidt在1979年提出。MUSIC演算法原理是從天線陣列所收到的訊號中求出輸入相關矩陣,並將輸入相關矩陣分解成兩個彼此獨立且正交(Orthogonal)的子空間(Subspace),分為訊號子空間(Signal Subspace)與雜訊子空間(Noise Subspace),利用正交特性去估測各個入射訊號的到達方向。使用MUSIC演算的前提是:入射訊號的數目要小於天線數目,並且訊號之間不能有相關性,才可得到較佳的解析度。
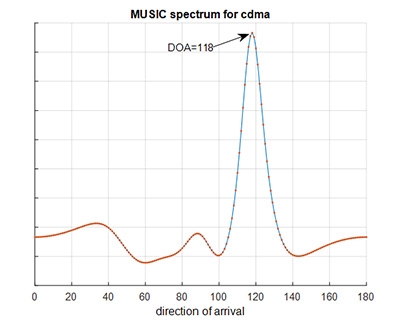 圖12 MUSIC演算法產生的空間頻譜
圖12 MUSIC演算法產生的空間頻譜
因追蹤向量與雜訊子空間互為正交,所以可得到MUSIC的空間頻譜(Spatial Spectrum)如公式5,其中Vn表雜訊向量子空間,a(𝜙)為陣列追蹤向量[3]。
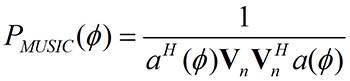
..............公式5
透過掃描MUSIC空間頻譜峰值(Peak)的方式,對所有可能的訊號來源方向進行搜索,可估測出多個入射到陣列天線的DOA,如果再結合展頻碼則可以辨識出唯一訊號的入射角(圖12),偵測出入射角是𝜙=118°,就可以使用共軛空間複數特徵法形成所需的輻射場型(圖13),其中陣列的N=8,𝜙=118°。
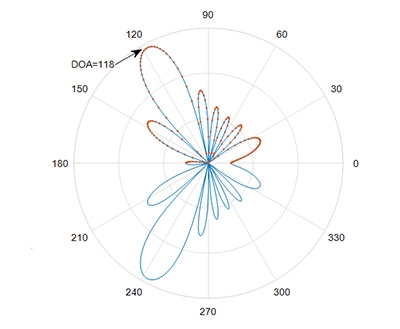 圖13 N=8的陣列的輻射場型
圖13 N=8的陣列的輻射場型
使用MUSIC演算法的缺點是,必須先從接收訊號中求出輸入相關矩陣,再對訊號相關矩陣作特徵值(Eigenvalue)與特徵向量(Eigenvector)分解,演算法所需的矩陣運算量較龐大且複雜度高。
(本文作者林福林任教於南台科技大學電子工程學系)