本文鎖定討論光柵波瓣(Grating Lobe)以及波束偏斜(Beam Squint)。由於光柵波瓣很難透過圖像解說,因此本文運用數位轉換器中的訊號映頻混擾,以及把光柵波瓣看作是一種空間混疊,藉由這些相似情況來進行解說。接著,再探討波束偏斜的問題。
波束偏斜是使用相位移技巧時導致天線出現頻率失焦,本文運用波束偏斜,而非真實時間延遲來操控波束。另外在此還會討論這兩種操控方法的優缺得失,以及瞭解波束偏斜在一般系統上產生的影響。
光柵波瓣
本文目前僅提到元素間隔d=λ/2的例子,圖1顯示在相位陣列中λ/2元素間隔常見的原因。圖中顯示兩個案例,第一個以藍色代表的案例是30°,接著d/λ間隔提高到0.7,來顯示天線場型如何變化。在這個間隔增加狀況中,造成波束寬度縮小,其產生了正面的結果。縮減各零陷點(Null)之間的間隔讓它們彼此更靠近,也能產生可接受的結果。接著本文看第二個角度,在這個案例中為負70o,產生了最不好的全陣列增益結果。這個天線增益的複本定義成一個光柵波瓣,也可視為空間映頻混擾(Spatial Aliasing)。
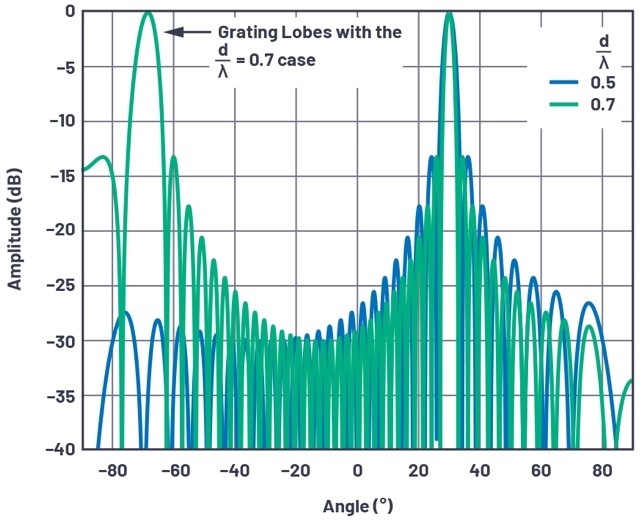 圖1 一個32元素線性陣列套用兩種不同d/λ間隔設定,經正規化之後的陣列因數
圖1 一個32元素線性陣列套用兩種不同d/λ間隔設定,經正規化之後的陣列因數
為方便瞭解光柵波瓣,本文以採樣系統中的映頻混擾作比喻。在類比至數位轉換器(ADC)方面,到了規畫接收器架構的階段,經常使用低額採樣方法。低額採樣涉及到降低採樣率(fS),透過採樣流程讓高於fS/2的頻率,屬較高奈奎斯特(Nyquist)區,像出現在第一奈奎斯特區的失真,造成這些較高頻率彷彿出現在ADC輸出端的較低頻率。
相位陣列的狀況也相當類似,各元素對波峰進行空間採樣。奈奎斯特理論可延伸到空間域,前提是每個波長中有兩個樣本-亦即元素,需要避免映頻混擾。因此,倘若元素間隔大於λ/2,能視為空間映頻混擾。
這些空間映頻混擾(光柵波瓣)究竟出現在何處?先前提到陣列各元素的相位差會與波束角成函數關係,如公式1。
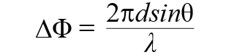
........................公式1
反過頭來,可推算出波束角和相位差成函數關係,見公式2。
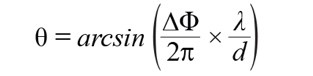
........................公式2
反正弦函數僅為引數產生介於負1與正1之間的實數解。若是超出上下限,求到的解就不是實數-這類似於試算表軟體的「#NUM!」函式。另外要注意的一點,是公式2中的相位是週期性,每2π重複一次。因此,本文可把∆Φ 換成波束操控公式中的 (m×2π+∆Φ),即得到公式3。
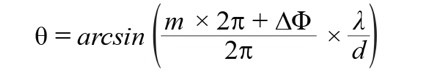
........................公式3
這裡的m=0、±1、±2…。
為防止出現光柵波瓣,本文的目標是求出一個實數解。就數學而言,用的方法是保持如公式4。
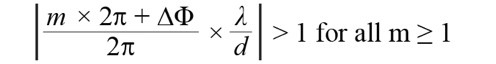
........................公式4
這麼一來,所有空間影像(亦即m=±1、±2等)就會產生非實數的反正弦結果,這些都可以忽略掉,但如果不能這麼做,一些m>0的值就會產生反正弦結果,最終得到多個解-結果就是光柵波瓣(見下圖2)。
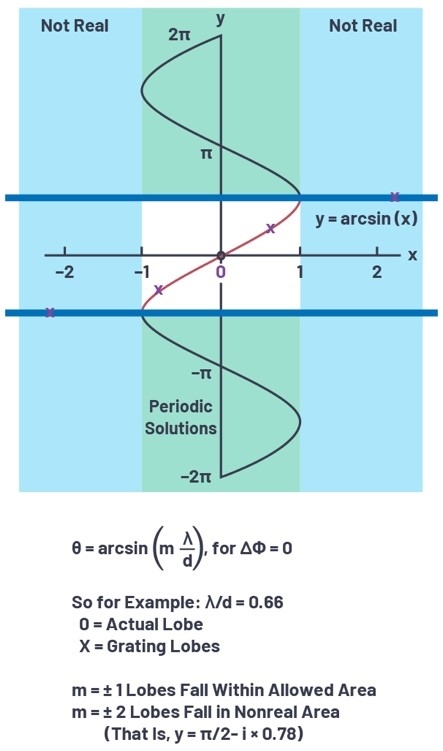 圖2 反正弦函數應用到光柵波瓣
圖2 反正弦函數應用到光柵波瓣
光柵波瓣在d>λ與λ=0°
這裡本文舉幾個例子以方便解釋。第一,在機械視軸的案例中,θ=0,而∆Φ=0。公式3可簡化成公式5。
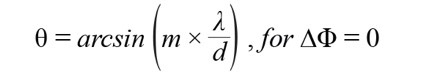
........................公式5
從這個簡化過程可證,若λ/d> 1,且m=0,則引數的上下限會在負1到正1之間。之後該引數會變成0,arcsin(0)=0°,亦即機械視軸角為0,符合本文的期望。此外,若m≥1,反正弦引數會太大(>1),得到的解就不是實數,當看到當θ=0而d<λ時不會產生光柵波瓣。
不過,若d>λ(因此λ/d就<1)能得到多個解,光柵波瓣便存在。舉例來說,若λ/d=0.66(因此d=1.5λ),當m=0以及m=±1時,就會存在反正弦實數解。m=±1則是第二個解,代表訊號的空間映頻混擾,預期能看到3個主波瓣,其振幅約略相等,出現位置分別在arcsin(0×0.66)、arcsin(1×0.66)、以及arcsin(-1×0.66)。在角度方面,分別是0o與±41.3o。事實上,這和圖3陣列因素圖所顯示的如出一轍(見下圖3)。
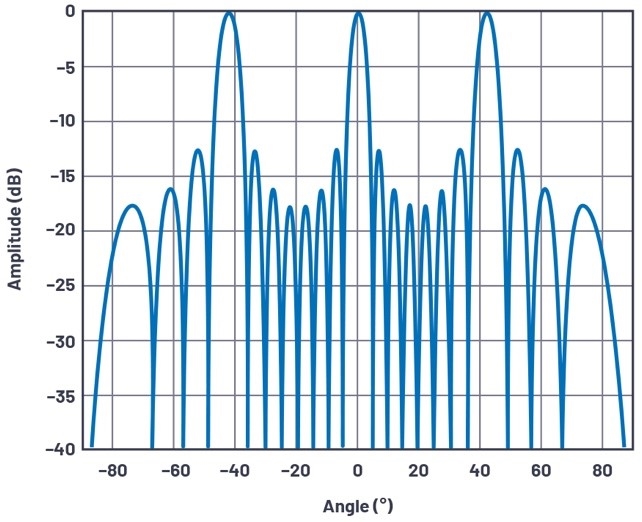 圖3 d/λ=1.5, N=8,在視軸處的陣列因素
圖3 d/λ=1.5, N=8,在視軸處的陣列因素
光柵波瓣在λ/2
在簡化光柵波瓣公式(公式5)方面,目前先選擇檢視機械視軸(∆Φ=0)。首先,在視軸方面,若d<λ便不會出現光柵波瓣。但就以採樣理論比喻來看,應該也預期得知,當間隔高過λ/2時將出現一些光柵波瓣。那麼當λ/2
首先,先前發現∆Φ的範圍從0到±π,相位隨著操控角一起改變,隨之變化的則是主波瓣偏離機械視軸。因此下列公式6,為變動範圍。
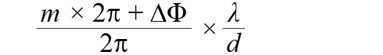
........................公式6
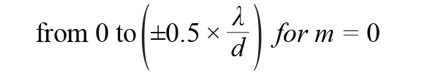
........................公式7
而當|m|≥1,總是會產生有一些效應(見公式8),
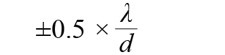
........................公式8
若是希望在所有|m|≥1的狀況讓整個反正弦引數維持>1,這就會限制了允許的最小λ/d值。在此需要考量兩種情況如下,
1.如果λ/d≥2(也就是說d≤λ/2),那麼不論m的值為何,都不會有多個解。所有m>0的解會產生一個反正弦引數>1。而這也是避免光柵波瓣出現在水平方向的唯一辦法。 2.但若刻意把∆Φ限制在小於±π的範圍內,能容許比較小的λ/d值,而且也不會看到光柵波瓣,縮減∆Φ的範圍意謂降低陣列的最大偏轉角。
元素間隔影響
因為天線研發業者必須考量一項取捨因素,元素間隔並非永遠小於λ/2。若是波束完全偏轉到水平,θ=±90o,需要λ/2的元素間隔(若在可視半球範圍不允許有光柵波瓣)。但實際上,最大可用的偏轉角永遠小於90°,因為元素因素和大偏轉角出現了其他退降(Degradation)。
從圖2中發現,若y軸θ局限在縮減的極限範圍,造成光柵波瓣只出現不會使用的掃瞄角。若特定元素間隔(dmax)而言,縮減極限(θmax)的目標是維持(見公式9)。
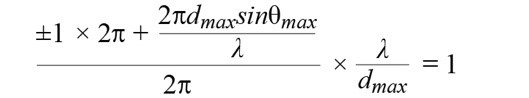
........................公式9
本文利用公式9計算出現第一個光柵波瓣(m=±1)的地方。從這項改變接著利用曾計算∆Φ的公式,即為公式10。
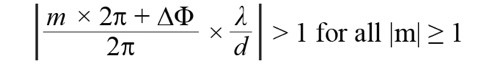
........................公式10
還可簡化成公式11。
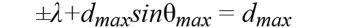
........................公式11
接著解算dmax(公式12)
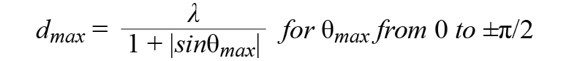
.........................公式12
dmax代表的狀況是縮減後的掃瞄角(θmax)沒有光柵波瓣,這裡的θmax小於π/2(90o)。舉例來說,倘若訊號頻率為10GHz,便會需要偏轉±50o而且不會出現光柵波瓣,那麼最大元素間隔則為公式13(見圖4)。
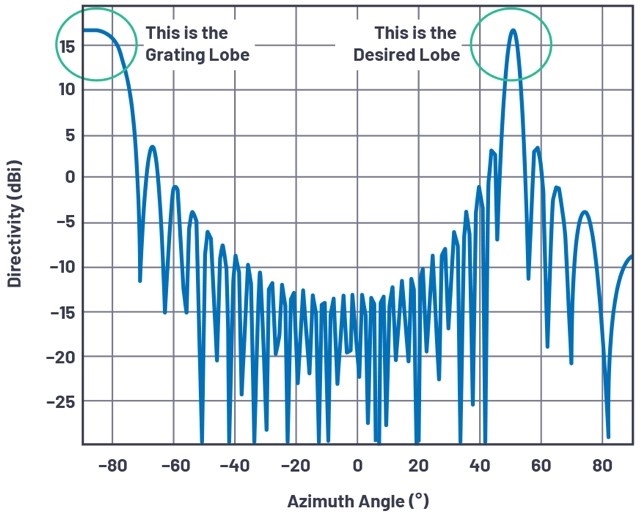 圖4 在θ=50o;N=32; d=17mm;Φ=10GHz的情況下,光柵波瓣開始出現在水平面上
圖4 在θ=50o;N=32; d=17mm;Φ=10GHz的情況下,光柵波瓣開始出現在水平面上
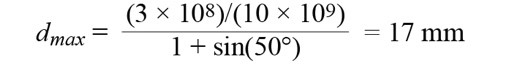
........................公式13
限制最大掃瞄角,便自由延展元素間隔,進一步增加每個通道的實體尺寸,也能延伸特定數量元素的孔徑。這種現象的應用範例,針對相當窄的預定方向指派一個天線,能增加元素增益,藉以朝預先定義方向提高指向性,此外也能增加元素間隔,來構成較大的孔徑。兩種結果則是在較窄的波束角內達到更高的整體天線增益。
注意到公式3顯示某個波長的最大間隔,包括在零偏轉角的狀況。這會發生在可視的半球中,不允許光柵波瓣的狀況。以地球靜止衛星(GEO Satellite)為例,從機械視軸來觀察,整個地球的偏轉角為9°,只要衛星不落到地表,或許可以容許光柵波瓣。在這類狀況中,元素間隔可能達到數個波長,導致波束寬度更窄。
另外,天線架構也是值得一提的面向,它能產生非均勻的元素間隔,協助克服光柵波瓣的問題,這些被歸類為非週期性陣列,其中,空間陣列就是明顯例子。基於組建機械式天線的各方面原因,業界希望利用通用型組件能夠擴充至更大的陣列,但這也可能產生一個均勻排列陣列,同時受到上述光柵波瓣狀況的限制。
波束偏斜
先前文章曾介紹波峰如何接近元素陣列,波峰角θ的元素和視軸之間存在時間延遲,在單一頻率情況下,可用相位移來取代時間延遲,藉以操控波束。這種方法雖然在窄頻波型有效,但寬頻波型中,波束操控是由相位移產生,而波束偏轉的方向與頻率成函數關係。由於時間延遲是一種線性相位移與頻率的關係,便直覺地將其解釋,因此對於波束方向而言,所需的相位移會隨著頻率函數改變,或者反過來說,對於相位移而言,波束方向會隨著頻率函數而改變,波束角隨著頻率函數改變,這種概念稱為波束偏斜(圖5)。
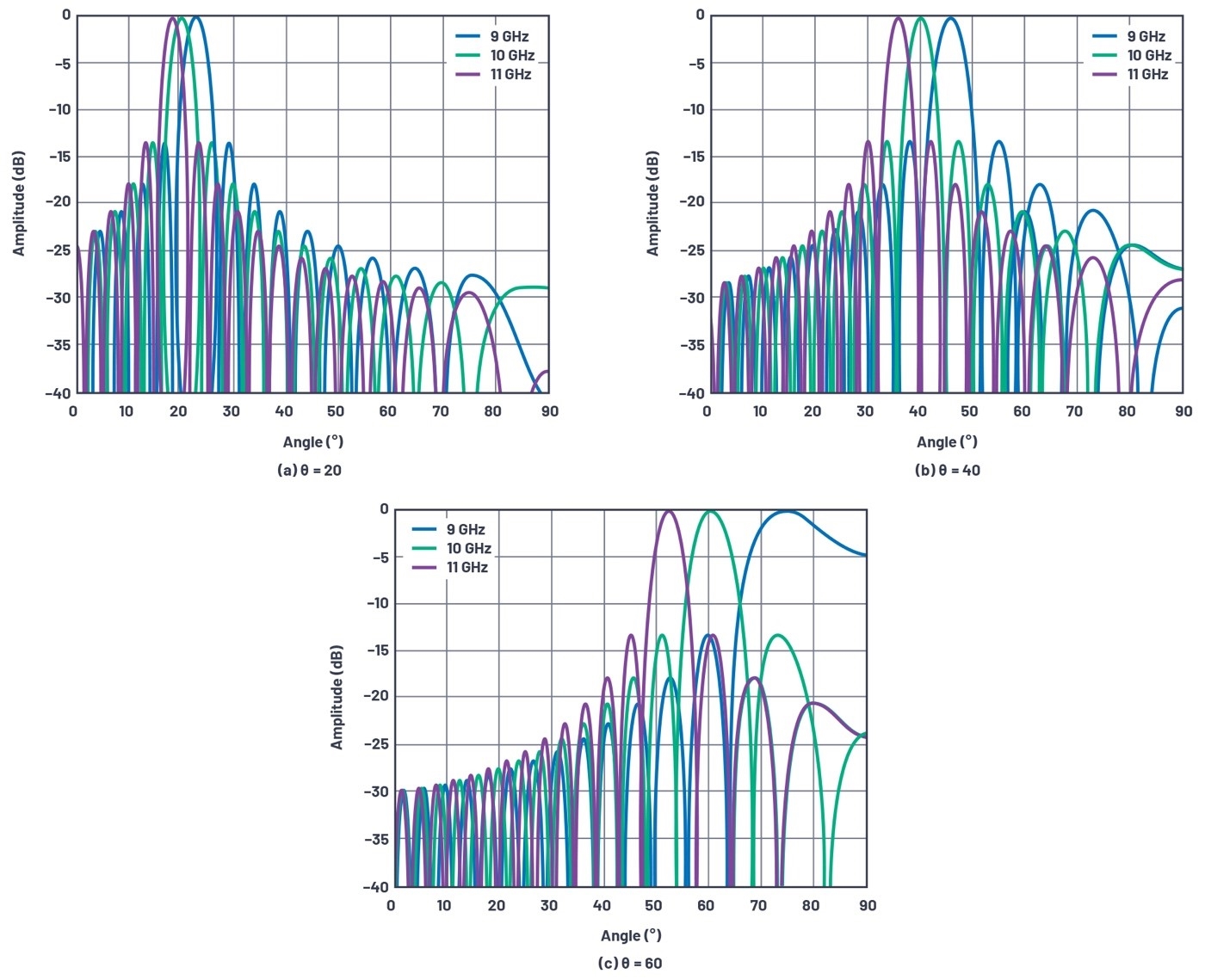 圖5 X波段上波束偏斜的例子,包含32元素線性陣列,採用λ/2元素間隔
圖5 X波段上波束偏斜的例子,包含32元素線性陣列,採用λ/2元素間隔
接著討論視軸的面向。當θ=0時,元素之間沒有相位移,便無法產生任何波束偏斜,因此,波束偏斜的量必須和θ角,以及頻率偏移呈函數關係。圖5顯示一個X波段的例子,在此例子中,中心頻率為10GHz,調變頻寬為2GHz,很明顯可看出波束改變方向與頻率以及初始波束角呈函數。
波束偏斜可直接計算。使用公式1與公式2,波束方向偏移、波束偏斜的計算公式為公式14。
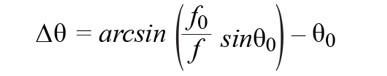
........................公式14
這個公式顯示在圖6。在圖6中,刻意顯示f/f0比值。前個公式的倒數(f0/f)提供一種更簡單的方法,以圖像呈現相對於中心頻率的變化。
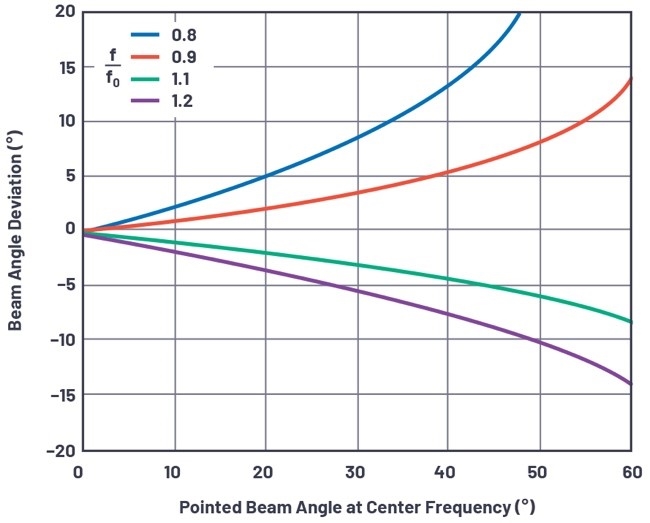 圖6 多重頻率偏移的波束偏移對比波束角
圖6 多重頻率偏移的波束偏移對比波束角
波束偏斜特性包括:波束角與頻率的偏離幅度,隨著波束角遠離視軸而加大;低於中心頻率的頻率,造成偏移的幅度大於比中心頻率還高的頻率所造成的偏移;低於中心頻率的頻率,把波束拖離視軸等。
造成波束偏斜、偏轉角與頻率的偏差,主要是相位移的時間延遲,然而,若利用真正時間延遲單元來建置波束操控,便有效地解決此問題。
既然如此,波束偏斜問題顯而易見,為何多數人仍選擇使用移相器而非時間延遲單元?大部份原因是移相器與時間延遲元件相比,具有設計簡易性和IC易得性的優點,時間延遲機制一般建置在傳輸線路方面,總共需要的延遲與孔徑尺寸成函數關係。目前為止,大多數在市面上的類比波束成形IC都以移相器為基礎,現今許多廠商也陸續推出真正時間延遲IC,在相位陣列建置方面逐漸普及化。
在數位波束成形方面,真實時間延遲機制可建置在DSP邏輯以及數位波束成形演算法。因此,每個元素進行數位化所依賴的相位陣列架構,自然就能克服波束偏斜問題,同時還提供可程式化的彈性。然而,解決方案的功耗、尺寸、以及成本都可能存在問題。
在混合波束成形中,結合配合子陣列的類比波束成形,以及配合全陣列的數位波束成形。這種方法在抵銷波束偏斜方面可以提供一定程度的效果,因此值得考慮採用。波束偏斜只受到子陣列影響,子陣列的波束寬度要大得多,因此也更能容許波束角偏移。因此,只要容許子陣列波束偏斜,混合式波束成形架構就能連同相移器進行建置,在此之後才是數位波束成形的真正時間延遲。
(本文作者為ADI技術經理、工程經理、資深應用工程師)
