數位通訊對通訊領域的工程師來說,仍然是一門相當複雜難懂的學科。作者從事通訊系統的教學已有相當一段時間,因此希望提供一套以MATLAB撰寫的數位通訊調變/解調程式集,以提供通訊工程師深入了解數位通訊理論及教學講解的方便性。目前程式已經撰寫及測試完成,程式集及操作說明檔可以提供有興趣的通訊相關工程師、老師及學生免費使用。
使用此套程式可輔助訊相關工程師對數位通訊的理解,例如功率放大器1dB壓縮點如何影響正交分頻多工(OFDM)/四相移鍵控(QPSK)訊號的品質,也可以幫助老師在數位通訊方面的教學講解,課後學生亦可透過程式做更深入的練習,希望此程式集對國內的通訊相關工程師及通訊教學方面能有所幫助。
本程式集包含兩個部分,第一個部分為各種基本的數位調變解調程式,第二個部分為簡單的展頻與OFDM範例。第一個部分包含的數位調變技術有:(1)二進位相移鍵控(BPSK)、(2)QPSK、(3)OQPSK、(4)MSK、(5)SRRC-π/4-DQPSK、(6)SRRC-16QAM、(7)BFSK、(8)4FSK、(9)GFSK。第二個部分則包含:(10)直接序列展頻(DSSS)/BPSK、(11)跳頻展頻(FHSS)/BFSK、(12)OFDM/QPSK。
本程式集利用MATLAB及其圖形化使用者介面(GUI)功能來製作數位解調教學軟體,調變解調功能採用基礎的MATLAB程式來完成,互動介面則使用GUI功能,分成互動主程式和被呼叫的副程式。
訊號在時間上是連續的,MATLAB程式則是離散的數值計算,如何把連續訊號以離散的形式來處理,如何把理論的概念以數學計算的方式來完成,這是程式撰寫最大的挑戰。另一個挑戰為圖形控制程式的撰寫,讓操作者在不懂MATLAB的情況下依然能夠輕鬆操作本程式集,而熟悉MATLAB及通訊理論的人則可以自己修改程式以符合研究或教學的需求。
了解程式集系統功能
第一個部分之調變部分可選擇的輸入如表1所示,輸出結果可看輸入資料(或IQ訊號)與調變訊號的時間波形,調變訊號的功率頻譜密度,調變訊號的向量圖(含星座圖)或相位樹圖。第一個部分之解調變部分可選擇的輸入如表2所示,解調的輸出結果可看眼線圖、接收調變訊號的功率頻譜密度,以及解調訊號的向量圖(含星座圖)或相位樹圖、解調訊號的誤差向量振幅(EVM)或頻率誤差。
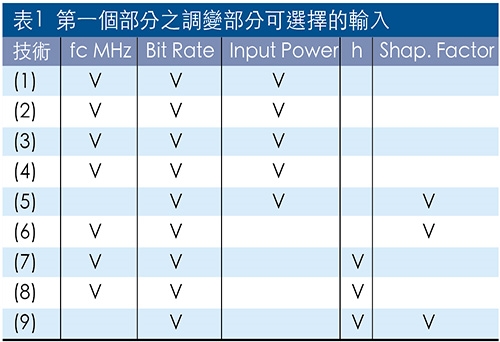
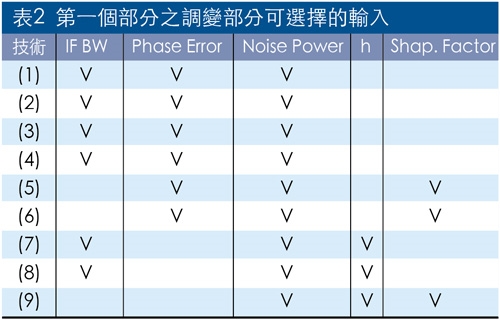
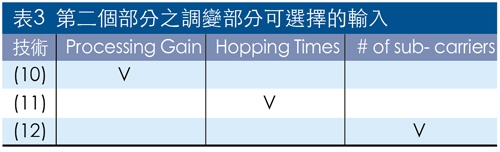
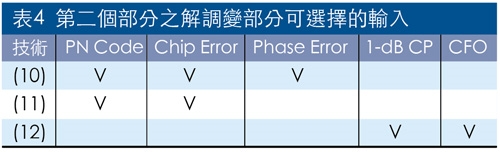
第二個部分之調變部分可選擇的輸入如表3所示,輸出結果DSSS/BPSK可看直序展頻與未展頻的功率頻譜密度,FHSS/BFSK則以動態方式直接看頻譜跳躍的情況,OFDM/QPSK則看功率頻譜密度與時間上的波形。解調部分可選擇的輸入如表4所示:解調的輸出結果可看眼線圖、接收調變訊號的功率頻譜密度,解調訊號的向量圖(含星座圖)或相位樹圖,解調訊號的EVM或頻率誤差。
GFSK調變/解調之程式概念介紹
以編號(9) GFSK的調變/解調為例,程式撰寫部分說明如下。首先是輸入參數設定,內容如下。其中,N=100為頻譜的寬度100MHz,Nl為1MHz裡面選取的點數,Nl=100代表1MHz裡面有100個點,也表示頻譜的解析度d=1/Nl=10kHz。Nop為絕對溫度T=290°的等效熱雜訊之功率頻譜密度,經過計算得出-114dBm/MHz,Nip為輸入雜訊之功率頻譜密度,在調變程式中Nip固定不變,但在解調程式中Nip可以改變數值:
Dr=1; % data rate (Mbps)
N=100; % N/2 : span (MHz)
Nl=100; % resolution in points/MHz
Nip=-110; % input noise floor (dBm/MHz)
Nop=-114; % equvelant theormal noise floor (dBm/MHz)
Fr=[5]; % center frequency of the carrier (MHz)
Frm=[-20]; % power of the carrier (dBm)
然後,進行GFSK數位調變參數設定:
h=.2; % modulation factor
bt=.5; % relative bandwidth for
Gaussian shaping
接著,做Butterworth BPF參數設定:
Bp1=[0 4 6 0 0 60 5]; % [* fl3 fh3 * * UATT order]
隨後,輸入資料轉成程式運算所需之變數。其中,lf表示對應的向量點數,其他算式則是用來準備後面所需要用到的參數,FT代表真實時間,FM代表橫軸頻率:
%%% source
lf=N*Nl; % total points
q2=sqrt(2); p2=2*pi; qN=sqrt(N); qk=lf/1000;
qf=sqrt(lf);ql=sqrt(Nl); rand('seed',56);
F=0:lf-1; Fh=F(1:lf/2); Fu=F/Nl;
FT=F/N; % time axis
FM=Fh/Nl; % frequency axis
接下來,產生未經shapping之基頻訊號:
dr=N/Dr; % number of points/bit
ds=lf/dr; % number of bits
dh=round(dr/2); ons=ones(1,dr);
for i=1:ds
Di((i-1)*dr+1:i*dr)=e(i)*ons;
end
再產生Gaussian Filter,而圖1為產生的Gaussian Filter之半邊轉移函數:
Dip=Di; bd=Dr*bt; io=bd*Nl; c=.347/io^2;
gau(1)=1;
for i=2:lf/2
gau(i)=exp(-c*(i-1)^2); gau(lf-i+2)=gau(i);
end
gau(lf/2+1)=gau(lf/2);
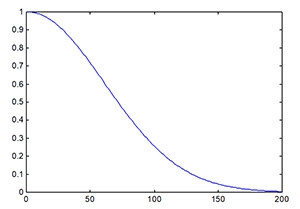 圖1 程式所產生的Gaussian filter之轉移函數
圖1 程式所產生的Gaussian filter之轉移函數
經由Gaussian filter濾波後之基頻段訊號,如下所示,而圖2為Gaussian Filter濾波後之基頻段訊號:
uf=fft(Di); uff=uf.*gau; Di=real(ifft(uff));
Dio=Di; Di=Di/dr*pi*h; U0=0;
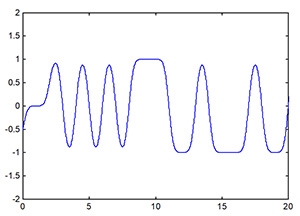 圖2 經由Gaussian filter濾波後之基頻段訊號
圖2 經由Gaussian filter濾波後之基頻段訊號
緊接著,產生Gaussian FSK調變訊號,公式1為數位FM產生的數學式:
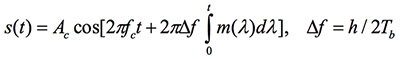
........................................................公式1
透過程式的輸出結果,如圖3所示:
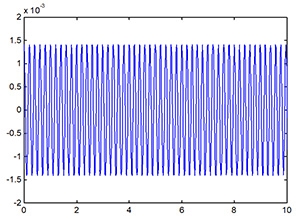 圖3 GFSK調變訊號之時間波形
圖3 GFSK調變訊號之時間波形
%%% GFSK generator
for i=1:lf
U0=U0+Di(i); Ui(i)=U0;
end
Fe=10^(Frm/20)*cos(p2*Fr*FT+Ui) /qf*q2; Fa=Fe;
然後,觀看GFSK訊號之功率頻譜密度。而圖4所示,則是GFSK調變訊號之功率頻譜:
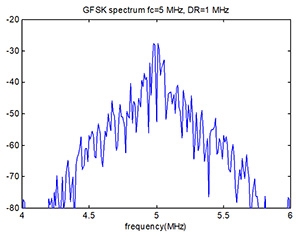 圖4 GFSK調變訊號之功率頻譜
圖4 GFSK調變訊號之功率頻譜
Faf=fft(so)/qf; Na=20*log10(abs (Faf));
Nb(1)=Na(1); Nb(2:lf/2)=Na(2:lf/2)+3;
接著,放大與濾波。在解調之前訊號會經過放大與濾波,放大器與濾波器已經以子程式的形式寫好,因此只要呼叫出來即可:
%%% 2nd AMP1
nt=2;G=A(1,nt); NF=A(2,nt); Pi3= A(3,nt); Pi2=A(4,nt);
csamp
%%% 1st stage: BPF1
Bp=Bp1; nt=1; G=A(1,nt); NF=A(2,nt);
csbpfbut
其中,csamp即是放大器子程式的名稱,內藏有IP2、IP3、雜訊指數及增益等參數,csbpfbut則是巴特沃夫濾波器子程式的名稱,內藏有級數、最大衰減量、置入損失等參數。緊接著,進行GFSK訊號解調,內容如下:
%%% GFSK demodulator
to=so.*exp(-j*p2*Fr*FT)/q2;
tfo=fft(to)/qf;
h0=1; sf=Dr*h0*2*Nl; tfz= zeros (1,lf);
tfz(1:sf)=tfo(1:sf); tfz(lf-sf:lf)=tfo (lf-sf:lf);
txo=ifft(tfz)*qf;
隨即,利用公式2算出相位角:
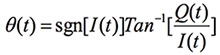
.................公式2
ang=angle(txo);
angtem=ang;
for i=1:lf-1
if ang(i+1)-ang(i)>5.6, ang (i+1:lf)=ang(i+1:lf)-p2;
elseif ang(i+1)-ang(i)<-5.6,
ang(i+1:lf)=ang(i+1:lf)+p2;
end
end
anh=ang*dr/(pi*h);
對相位角微分可以得到瞬時頻率,計算時是利用離散的差分取代公式3的微分:
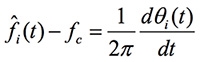
......................公式3
fui=diff([anh(1) anh]);
Fui=fui(dh+1:dr:lf);
Dui=Dio(dh+1:dr:lf);
瞬時頻率與原始正確頻率相減即為瞬時頻率誤差,可使用公式4:
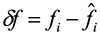
....................................公式4
ss=Fui-Dui; lss=length(ss); ss=ss(2:lss);
再透過公式5,由均方根計算可以得到平均頻率誤差:
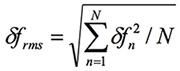
........................公式5
ferr=sqrt(ss*ss')/(lss-1);
最後,將結果畫圖。圖5為輸入功率-60 dBm時之模擬結果,頻率誤差約為5%。
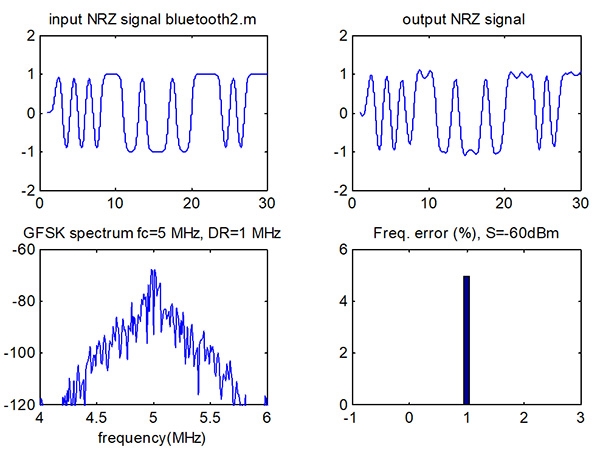 圖5 輸入功率-60 dBm時頻率誤差約為5%
圖5 輸入功率-60 dBm時頻率誤差約為5%
教學軟體操作步驟示範
每一項調變技術對應到一個檔案夾,底下以編號(3) OQPSK為例,說明程式操作的步驟及對應的輸出結果。
首先,打開MATLAB程式,然後透過MATLAB打開OQPSK檔案夾內的gaoqpsk_exe.m程式。執行gaoqpsk_exe.m程式後,此時螢幕右下角會彈跳出一個操作視窗(圖6)。
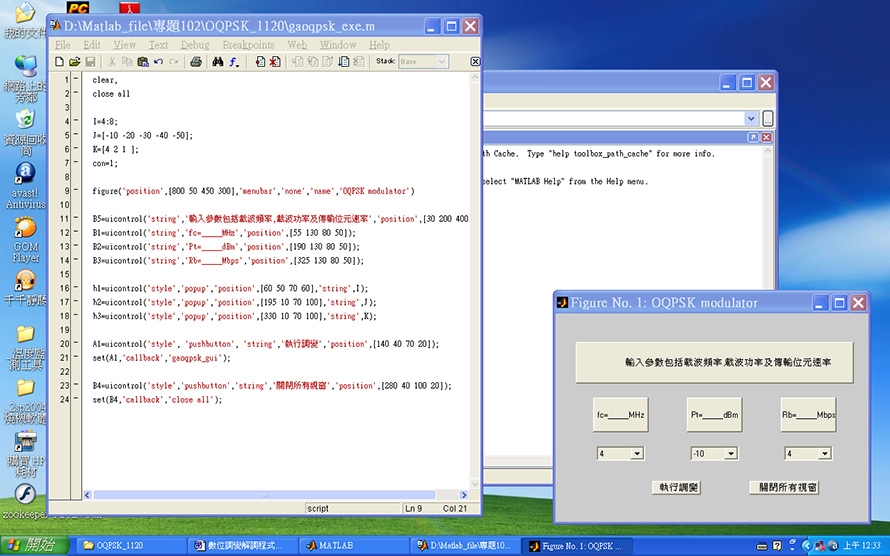 圖6 螢幕右下角彈跳出操作視窗
圖6 螢幕右下角彈跳出操作視窗
參數開始定義為載波頻率4MHz、載波功率-10dBm、位元傳輸速率4Mbps,再按下〔執行調變〕按鈕,將得到如圖7所示的輸出結果,其中左上圖為I-data與Q-data,與I-data相比,Q-data在時間上延遲了半個符號時間(Symbol Time);右上圖為OQPSK調變訊號的時間波形,可以觀察到某些時間點會有相位的突然改變;左下圖則是星座圖(含向量圖),很明顯地看到向量圖不會穿越原點;而右下圖為功率密度頻譜,零點到零點頻寬恰為符號速率的兩倍( )。
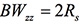
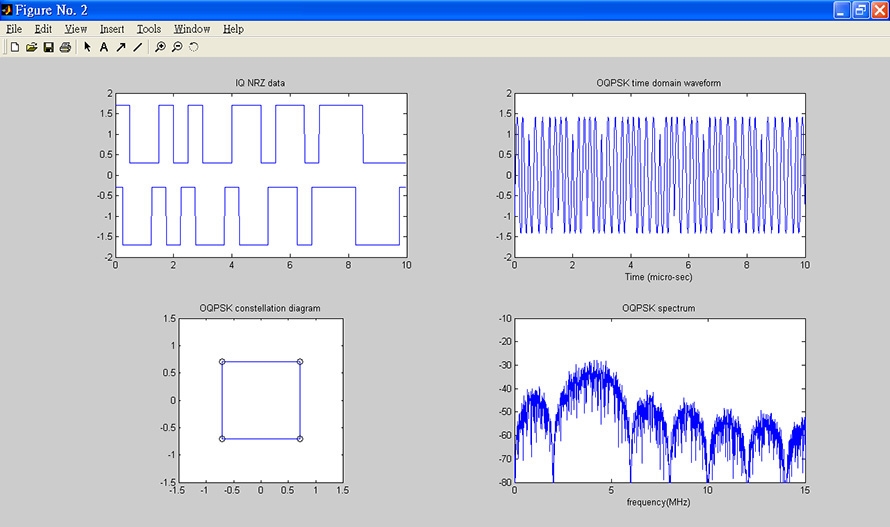 圖7 得到輸出結果
圖7 得到輸出結果
然後,利用下拉式的選擇按鈕,改變載波頻率成為8MHz,按下〔執行調變〕按鈕,得到的輸出如圖8所示,可以看到頻譜的最高點由原來的4MHz移到8MHz。
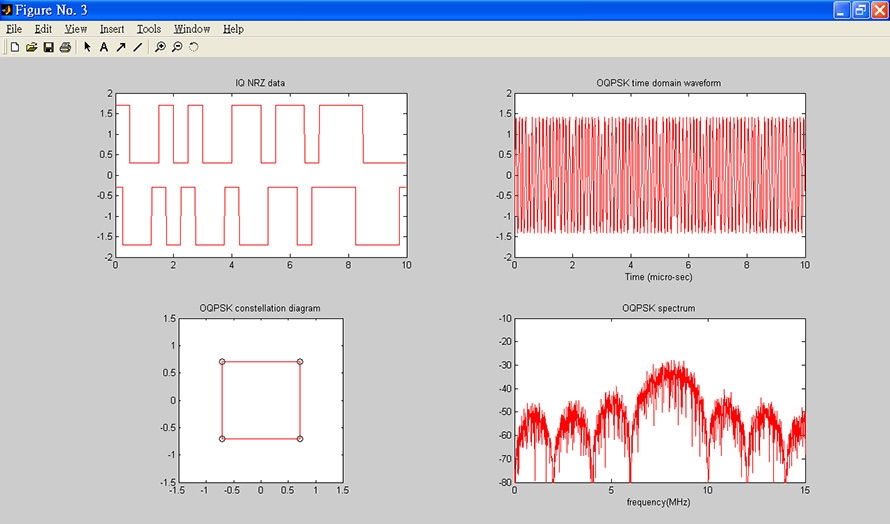 圖8 頻譜的最高點由原來的4MHz移到8MHz
圖8 頻譜的最高點由原來的4MHz移到8MHz
再利用下拉式的選擇按鈕,改變位元傳輸速率成為2Mbps,按下〔執行調變〕按鈕,得到輸出如圖9所示,可以看到零點到零點頻寬縮小成原來的一半。隨後按下〔關閉所有視窗〕按鈕,結束OQPSK調變程式。
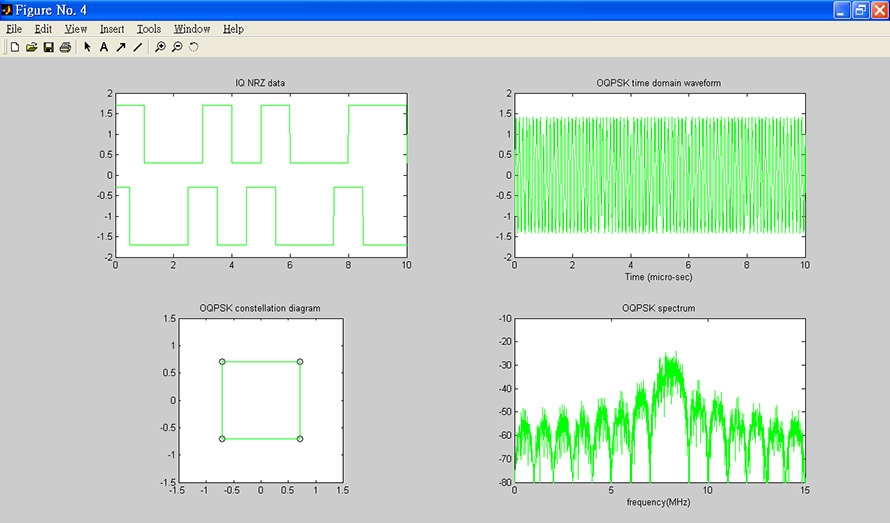 圖9 零點到零點頻寬縮小成原來的一半
圖9 零點到零點頻寬縮小成原來的一半
接下來,透過MATLAB打開OQPSK檔案夾內的deoqpsk_exe.m程式。執行deoqpsk_exe.m程式後,此時螢幕右下角將彈跳出一個操作視窗。隨後,參數開始定義為3dB中頻頻寬6MHz,雜訊功率頻譜密度-80dBm/MHz,本地振盪器相位誤差0度,再按下〔執行解調〕按鈕,得到輸出如圖10所示,其中左上圖為解調後I-訊號與Q-訊號的眼線圖,右上圖為星座圖(含向量圖),左下圖為功率密度頻譜,原始定義為載波頻率6MHz,中頻載波功率-20dBm,位元傳輸速率2Mbps,而右下圖是向量誤差振幅值(EVM),在此例中,EVM為失真程度很低的1.93%。
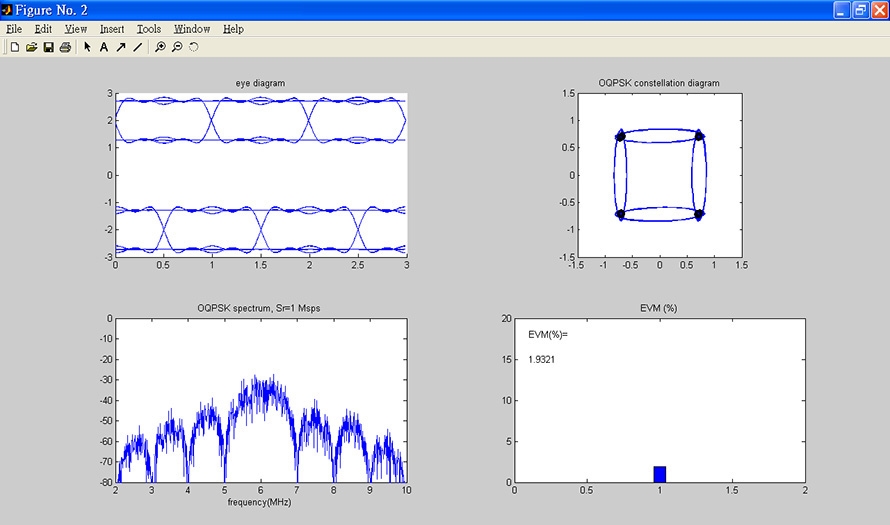 圖10 顯示輸出結果
圖10 顯示輸出結果
再利用下拉式的選擇按鈕,改變3dB中頻頻寬成為2MHz。按下〔執行解調〕按鈕,得到的輸出如圖11所示,EVM為5.01%,可以看到降低中頻頻寬已經讓解調訊號的品質變差(1.93%=>5.01%)。
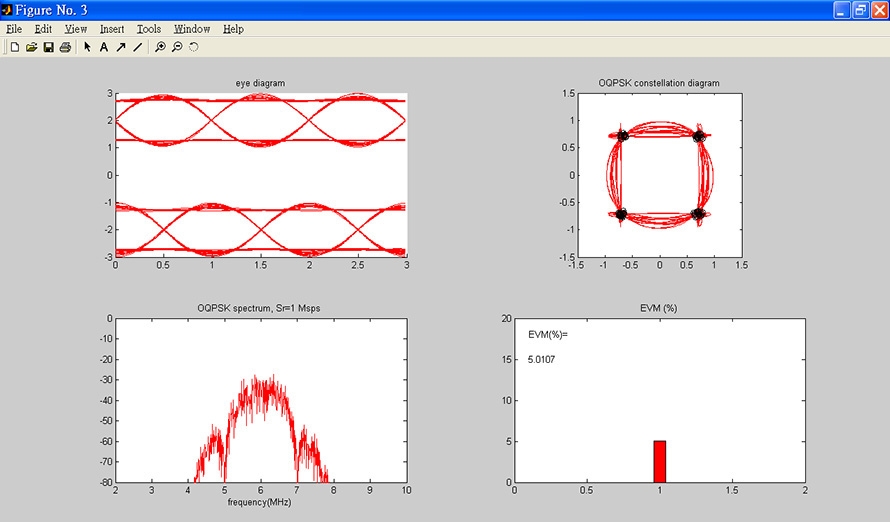 圖11 降低中頻頻寬讓解調訊號的品質變差
圖11 降低中頻頻寬讓解調訊號的品質變差
將中頻頻寬改回6MHz,改變雜訊功率頻譜密度成為-60dBm/MHz,按下〔執行解調〕按鈕,得到輸出如圖12所示,EVM為4.03%,可以看到增加雜訊功率降低了解調訊號的品質(1.93%=>4.03%)。
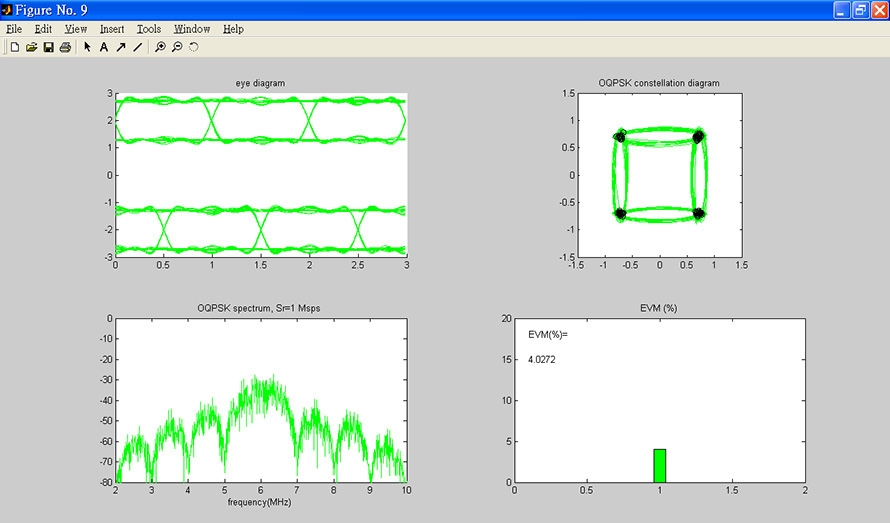 圖12 增加雜訊功率會降低解調訊號的品質
圖12 增加雜訊功率會降低解調訊號的品質
接著,將雜訊功率頻譜密度改回-80dBm/MHz,改變相位誤差成為10度,並按下〔執行解調〕按鈕,得到輸出如圖13所示,EVM為17.58%,可以看到本地振盪器的相位誤差降低了解調訊號的品質(1.93%=>17.58%)。最後,按下〔關閉所有視窗〕按鈕,結束OQPSK解調程式。
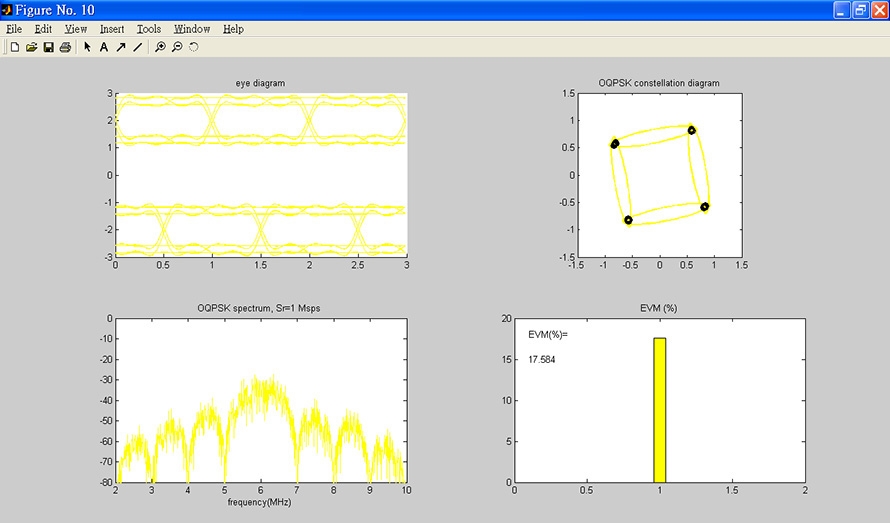 圖13 本地振盪器的相位誤差降低了解調訊號的品質
圖13 本地振盪器的相位誤差降低了解調訊號的品質
判讀部分軟體輸出結果
以下透過DSSS-BPSK解調、OFDM/QPSK調變解調兩部分來說明部分軟體的輸出結果。
DSSS-BPSK解調
以編號(10) DSSS-BPSK之解調為例,來討論程式操作的輸出結果。內部參數定義為載波中心頻率35MHz,符元傳輸速率sps,發射端PN碼編號為1,處理增益PG=15,假設選擇接收端PN碼編號為1,同步碼誤差時間為0,載波相位誤差為0,按下〔執行解調〕按鈕,得到輸出如圖14所示。其中,左上圖為解調之眼線圖,可以觀察到在判斷點的眼睛有清楚的外型,而左下圖為直序展頻的功率密度頻譜。右上圖黑色小圈圈為星座圖,很明顯地座落在±1的位置,對應到BPSK的星座圖。而右下圖為誤差向量振幅值,EVM=4.79%表示解調結果之誤差很小。
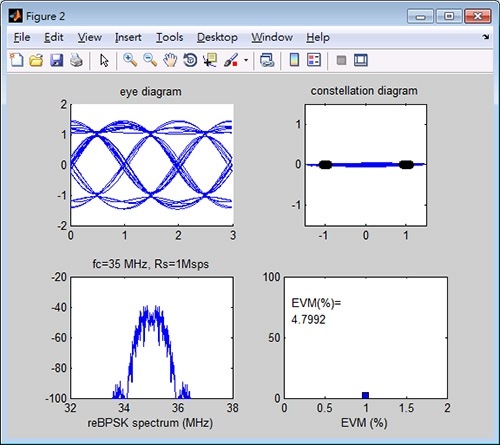 圖14 PN碼編號為1,碼時間與載波相位誤差為0。
圖14 PN碼編號為1,碼時間與載波相位誤差為0。
為顯示不同的PN碼無法正確的解直序展頻,將接收端PN碼編號設為2,結果如圖15所示,解調結果之EVM暴衝至200.69%,表示不正確的PN碼無法成功解直序展頻。 即使接收端PN碼編號正確,但收發碼之間若無法完全同步,解調結果也會產生極大的失真,將接收端PN碼編號恢復為1,同步碼誤差之細片時間設為0.5,結果如圖16所示,解調結果之EVM=11.61%,表示不正確的同步碼時間會造成解調的誤差擴大。
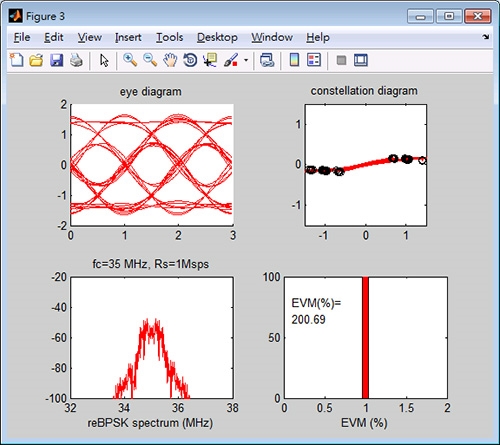 圖15 PN碼編號為2(不同的PN碼)
圖15 PN碼編號為2(不同的PN碼)
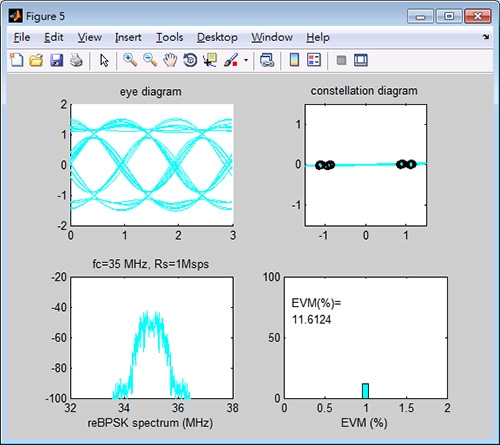 圖16 同步碼時間誤差為0.5
圖16 同步碼時間誤差為0.5
即使接收端PN碼編號正確,收發碼之間也完全同步,但載波卻有相位誤差10度,解調結果也會產生極大的失真,將接收端PN碼編號恢復為1,同步碼誤差之細片時間設為0,結果如圖17所示,解調結果之EVM= 18.46%,表示相位誤差會造成解調的誤差。
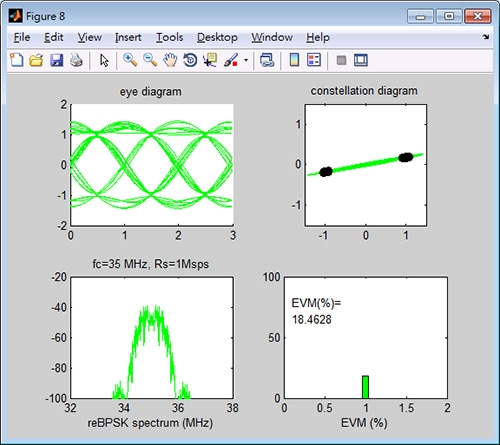 圖17 載波相位誤差為10度
圖17 載波相位誤差為10度
OFDM/QPSK調變解調
再以編號(12) OFDM/QPSK調變/解調為例,先看調變的結果:參數中子載波個數設為4,執行結果如圖18所示,圖中的上半部為OFDM/QPSK功率頻譜密度;下圖為OFDM/QPSK調變訊號在時間上的波形,OFDM訊號是由多個相位鍵移(Phase Shift Keying, PSK)或正交振幅調變(Quadrature Amplitude Modulation, QAM)的子載波組合而成的,本程式集選擇QPSK,之後再乘上各子載波相加即為OFDM訊號。
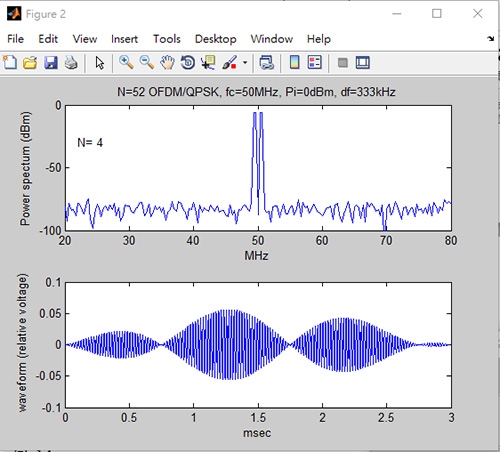 圖18 子載波個數設為4的OFDM/QPSK調變結果圖
圖18 子載波個數設為4的OFDM/QPSK調變結果圖
之後,把OFDM/QPSK的調變參數子載波各數做一些改變,比較一下各圖的差異與細節討論。把子載波各數4改變成52,如圖19所示,之後與圖18的OFDM/QPSK調變結果參考圖來做個比較,可以看到功率頻譜密度與調變訊號時間上的波形明顯地起伏變化。
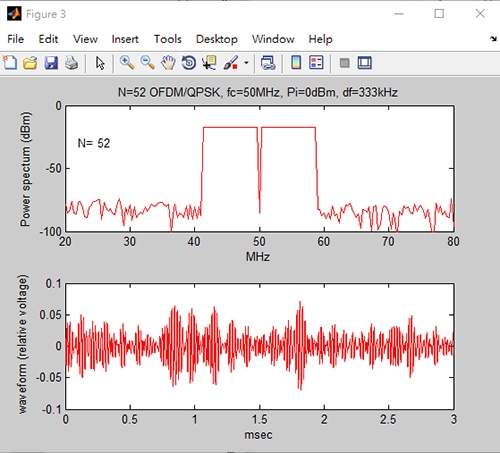 圖19 子載波個數更改為52的OFDM/QPSK調變結果圖
圖19 子載波個數更改為52的OFDM/QPSK調變結果圖
然後,再看解調的結果。假設選擇功率放大器之1dB壓縮點P1dB=20dBm,載波頻率偏移CFO=0%,得到輸出如圖20所示,其中左上圖為OFDM訊號之時間波形,可以觀察到劇烈變化的外型輪廓。而左下圖為功率密度頻譜,很明顯地看到頻譜的中心是空的。右上圖則為星座圖,紅色十字是發射端訊號的星座圖,黑色圓圈則是解調結果,與發射端相當吻合。右下圖為誤差向量振幅值,EVM=3.1032%表示解調結果誤差很小。
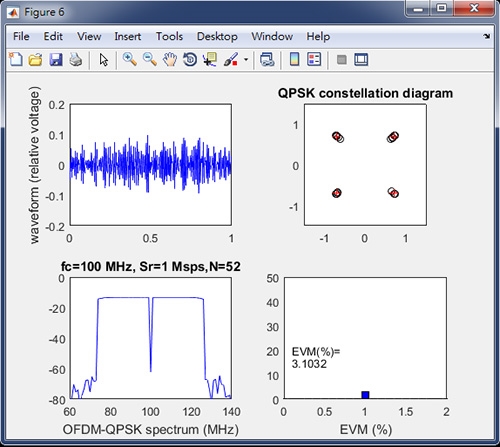 圖20 正常的OFDM/QPSK解調之各種結果
圖20 正常的OFDM/QPSK解調之各種結果
為了顯示放大器的線性度對OFDM波形失真的影響,將功率放大器之1dB壓縮點降為P1dB=10dBm,結果如圖21所示,解調結果為EVM=4.8496%,結果表示1dB壓縮點越小,解調訊號誤差越大。
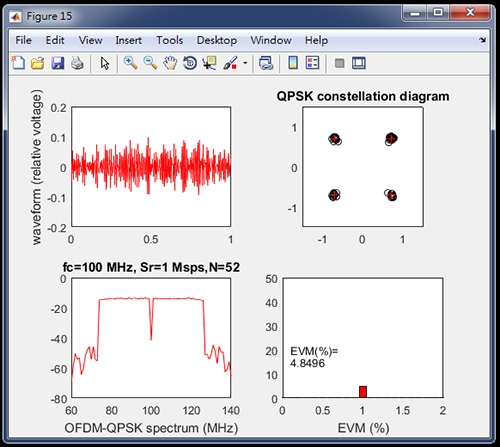 圖21 當P1dB=10dBm之解調結果
圖21 當P1dB=10dBm之解調結果
針對顯示載波頻率偏移(Carrier Frequency Offset, CFO)對OFDM解調的影響,把功率放大器之1dB壓縮點恢復成原來的P1dB=20dBm,載波頻率偏移則設為CFO=10%,結果如圖22所示,解調結果為EVM=35.6739%,表示載波頻率偏移會造成解調的誤差擴大。
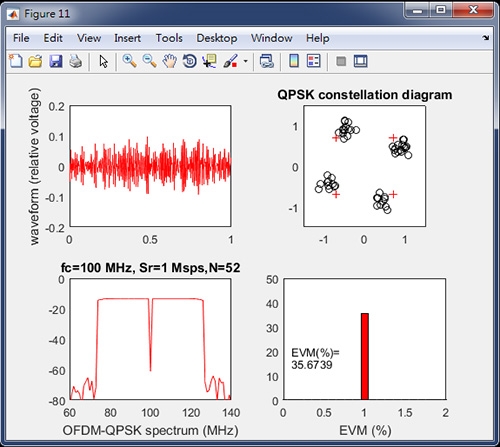 圖22 存在CFO=10%之解調結果
圖22 存在CFO=10%之解調結果
分析數位調變訊號 分辨箇中特性/差異性
本篇文章利用MATLAB來製作調變和解調教學軟體,經由模擬可清楚了解各種數位調變訊號的特性與差異性。如果對程式撰寫相當熟悉,則可以到程式集裡自行修改想要的其他輸入參數,修改完成後,再重新命名並執行,就可以呈現出自己想要的輸出結果,期望這套程式集對想進一步深入了解各種數位調變解調的通訊相關人員有所幫助。
(本文作者為南台科技大學電子工程學系助理教授)