無線定位的目標在於,如何在無線通訊系統下精確估測行動台的位置。當有非視距誤差影響下,各個量測有大量誤差時,將導致行動台周遭偵測能力不佳。在這些情況下,必須把多個合理的量測綜合起來,以獲得更精準的估測。
本文將提供一個抵達時間與抵達角度的混合估測方法,利用抵達時間與抵達角度方程式形成的交點,經過權重計算的分析,來獲得行動台位置的估測,而不需要非視距誤差的事先機率統計分析。模擬結果也顯示,在不同的非視距誤差模式下,提出的方法比起相關的方法,有著較高的精準度。
無線定位在近幾年獲得許多注意與討論,其包含許多方法如抵達角度、抵達時間、抵達訊號強度以及抵達時間差。高精確定位可視為量測到行動台與基地台的視距距離;但由於訊號傳輸會遭遇反射與繞射,非視距誤差幾乎都會存在,造成時間與角度量測的大量誤差,嚴重降低定位的精準度。
時間量測方法包含抵達時間與抵達時間差兩種,在二維(2D)平面上,至少需要三個基地台量測。而角度量測方法利用天線陣列偵測訊號量測到的抵達角度,只需要兩個基地台。一般來說,時間量測比角度量測具有較高的精確度,而時間與角度的混合法綜合以上兩種量測方法,以獲得更高精確的行動台位置估測。
偵測力(Hearability)是另一個議題,會影響無線定位技術的選擇方法。偵測力被定義為行動台能夠同時偵測到多少周遭的基地台,換句話說,行動台能收到多少大於一定程度的訊雜比以上的基地台資訊。
舉例來說,如果行動台太靠近服務基地台,則行動台很難收到除了服務基地台外其他周遭的基地台訊號,造成偵測力不佳;另一例是,行動台在鄉下偵測力不佳,由於在鄉下地區,每個基地台覆蓋的服務範圍都十分廣大。在大部分的實際狀況下,行動台能偵測到的基地台為二至三個,若是只有兩個,就必須藉由抵達角度量測的輔助。以下討論將設定在只能偵測到兩個基地台,但兩個基地台皆具有抵達時間與抵達角度的量測。
由幾何觀點來看,抵達時間量測,會形成以基地台為圓心的一個圓;而抵達角度則是以一個某個量測到的方向,形成通過基地台的一條直線。這些圓與線會在2D平面上形成許多交點,這裡提出幾何分析法,以權重與排序的方法來分析這些交點的資訊。模擬結果顯示,無論在何種情形下,該演算法明顯優於泰勒級數演算法與混合線演算法這兩種傳統的定位方法。
以多基地台估測行動台位置
假設抵達時間與抵達角度皆為精準無誤,則只需要一個基地台的資訊即可得知正確行動台的位置。但實際上,量測會因為非視距效應而出現誤差,因此需要多個基地台來估測行動台位置。
假設現在有兩個量測時間資訊與兩個基地台的抵達角度資訊,在不失一般性的假設下,假設兩個基地台的座標為(X1,Y1),(X2,Y2),則兩個基地台到行動台的量測距離可以表示成:
.................公式1
(x,y)表示行動台的位置,c為光速,ti則是基地台所量測到的抵達時間。另外,假設θ為行動台與服務基地台量測到的抵達角度(以x軸為參考方向):
.................公式2
傳統定位方法精確度有虞
以下就泰勒級數演算法和混合線演算法兩種相關定位方法,分別加以說明。
| ‧ |
|
| |
泰勒級數演算法是一個疊代的演算法,利用泰勒級數將抵達時間的方程式線性化,從一個初始的預測位置開始,之後進行疊代的動作。假設(Xν,Yv)是初始的預測,則泰勒級數演算法可表示為下列的數學式:
最後利用最小平方差解(Least Square Solution)獲得估測行動台的位置,。泰勒級數演算法的最大問題在於,一開始預測的行動台位置並不精確,有可能會造成演算法的收斂問題。 |
| ‧ |
|
| |
混合線演算法是將抵達時間與抵達角度量測的方程式寫成矩陣型式,最後利用最小平方差解獲得估測行動台的位置。 |
幾何分析定位法說明
藉由抵達時間,就可以推算出行動台與基地台間的距離。由幾何觀點來看,抵達時間量測會形成以基地台為圓心的一個圓,其半徑即為抵達時間換算成的距離。抵達角度則是利用天線陣列或方向天線去偵測訊號抵達的角度,而在幾何觀點中,抵達角度會形成通過基地台的一條直線。在行動台擁有兩個抵達時間與兩個抵達角度的情況下,在不失一般性的假設下,假設兩個基地台的位置分別為(0,0)與(X2,0),如圖1所示。那麼兩個抵達時間與兩個抵達角度的方程式可以表示為:
Circle 1: x2+y2=r12 .................公式3
Circle 2: (x-X2)2+y2+=r22.................公式4
Line 1: tanθ1.x-y=0.................公式5
Line 2: tanθ2.x-y=tanθ2.X2.................公式6
一般來說,如果沒有非視距誤差,這些圓與線會交會於正確行動台位置上,但實際上非視距效應始終存在。由於非視距效應,訊號無法以直線距離傳輸,而量測到額外的距離,會對抵達時間造成正值的誤差;而對於抵達角度會造成角度偏移。
圖1顯示一個幾何表示,真正的行動台位置會坐落在兩圓交集的範圍內:F-F'。在這範圍裡面的交點,此處定義為「合適交點」,方程式形成的點經過合適交點條件篩選後,才會進到下一步的幾何分析法作分析。接著介紹五種幾何分析法的方式:
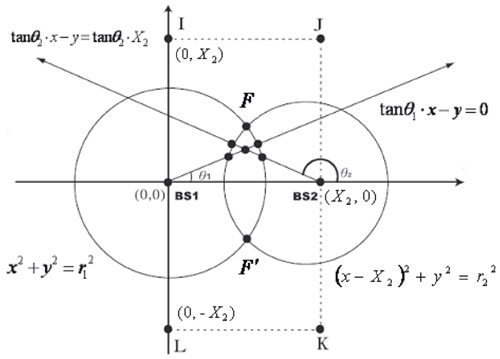 |
| 圖1 二圓二線的幾何分布圖 |
| ‧ |
|
| |
將所有合適交點取平均值(XN,YN),平均值(XN,YN)即為估測的行動台位置:
|
...............公式7
| ‧ |
|
| |
共分三個步驟,首先,步驟一同平均法,將所有合適交點取平均值(XN,YN),然後步驟二計算各合適交點與平均值(XN,YN),的距離di:
...............公式8
步驟三則以(di2)-1為權重,求得估測位置。最後的行動台估計位置可以表示成:
...............公式9
|
| ‧ |
|
| |
共四個進行步驟,步驟一與步驟二同距離權重法。而步驟三,將合適交點依照di的大小,遞增進行排列。步驟四則取前M個合適交點做平均值,獲得估計行動台位置:
|
......公式10
| ‧ |
|
| |
有四個步驟,步驟一至步驟三同排序平均法,步驟四起,以(di2)-1為權重,取前M個合適交點做平均值,獲得估計行動台位置:
|
......公式11
| ‧ |
|
| |
步驟一先計算兩兩合適交點間的距離dmn(1≦m,n≦N);步驟二為選擇一個界限值Dthr,這裡取的是所有dmn的平均值;步驟三,設定一個權重Ik,1≦k≦N,一開始起始值均為零。若dmn≦Dthr,則將權重增加Im=Im+1、In=In+1(1≦m, n≦N);最後的步驟四,則最後的行動台估計位置可以表示成:
|
......公式12
由模擬結果比較優劣
模擬結果為假設在未知非視距效應的統計特性前提下,分別針對不同方法進行一萬次的試驗,兩個基地台的座標設為(0,0)、(2000m,0),行動台的位置則隨機坐落於I、J、K、L的四邊形中,同圖1所示。
第一個誤差模型稱作圓盤狀散射點模型(Circular Disk of Scatterers Model, CDSM),圓盤狀散射點模型假設基地台與行動台的傳輸間存在一個散射點,此散射點坐落於行動台周圍的某個半徑上;由於散射點的干擾,抵達時間與抵達角度都會有所誤差。
在兩圓兩線的情況下,採用兩個基地台皆為散射半徑為200公尺(m)的假設,來檢驗各個演算法的優劣。如圖2所示,相較於兩種相關演算法,此處提出的五種幾何法都有較好的表現,且不分軒輊。
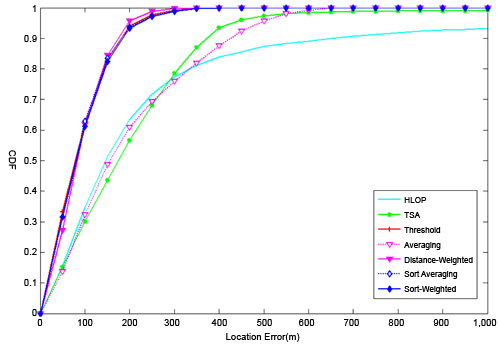 |
| 圖2 二圓二線在CDSM模型下的累積機率分布圖 |
此外,另一種比較方法為,在CDSM誤差模式下,在不同的散射點的半徑下的均方根誤差,當散射點的半徑增加時,也就是非視距效應加劇時,定位的精確度會不斷下降。
圖3顯示,在二圓二線的條件下,同樣假設兩個基地台的散射半徑則分布在100~500公尺時,各種演算法的均方根誤差值。相較泰勒級數與混合線演算法,即使是在非視距效應加劇時,這裡提出的演算法能夠有效抵抗非視距效應的影響,提供更準確的位置估測。
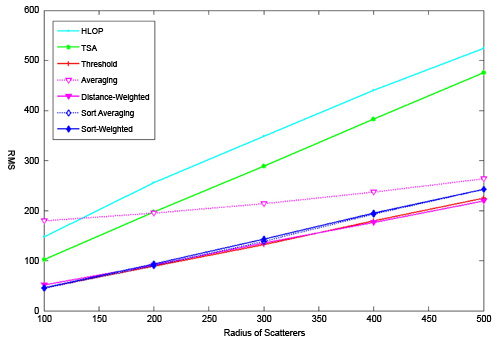 |
| 圖3 二圓二線條件下,不同方法下的均方根誤差比較 |
第二種誤差模式稱作偏移均勻分布模型,假設量測時間可以寫為ηi=pi+ui.qi,pi與qi為一個常數,ui則為一個均勻分布函數於[0,1];抵達角度誤差同樣相似地,可以寫為IfiI=αi+ui.βi,αi與βi為一個常數。兩個基地台的誤差參數如下:p1=50m、p2=150m、q1=q2=200m、α1=2.5°、α2=3°及β1=β2=5°。如圖4所示,用累積機率分布圖來表示,以上介紹的幾種幾何定位法依然能夠表現地較兩種傳統演算法優異。
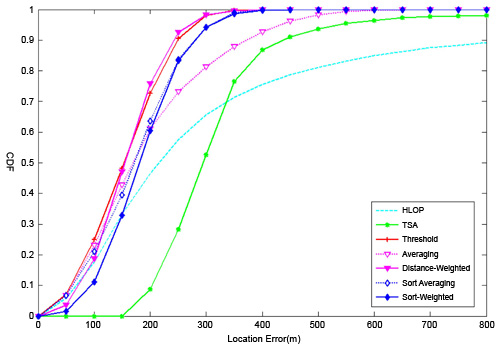 |
| 圖4 偏移均勻分布之各種方法的累積機率分布圖比較 |
最後一種誤差模式稱做均勻分布模型,其誤差模型假設量測時間的誤差為均勻分布於(0,Ui),其中,Ui又稱做量測時間的誤差上限;而抵達角度誤差則是假設為fi=Wi.τi,Wi為均勻分布函數於[-1,1]。
若用累積機率分布圖來表示,其中U1=300m、U2=400m、τ1=5°、τ2=10°。如圖5所示,從中可以發現,泰勒級數與混合線演算法表現較差,距離權重法則有最佳的表現,接著是界線值法。
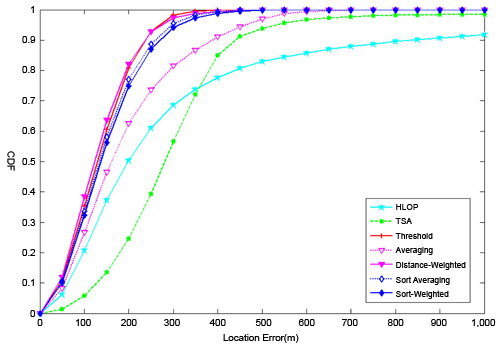 |
| 圖5 均勻分布之各種方法的累積機率分布圖比較 |
(本文作者依序為台南科技大學網路與資訊中心主任、成功大學電腦與通訊研究所研究生、高雄應用大學資訊管理研究所研究生)