GPS單點定位可以使GPS接收器快速獲得精準座標,然而,由於GPS衛星和接收器之間具有多種潛在干擾因素,導致GPS單點定位技術測量精確度最多只能達到公尺級別。為了提高精確度,必須再採用相對定位技術來輔助單點定位技術,以將精確度提高至公分等級。
理論上,如圖1所示,GPS單點定位(Point Positioning)是最直接可以使GPS接收器快速獲得精準座標的技術。然而,由於GPS衛星和接收器之間的時脈誤差、接收器的雜訊、多路徑誤差(Multipath Error)、電離層(Ionosphere)和對流層(Troposphere)的干擾(圖2)等未知變數,導致GPS單點定位技術在測量的精確度上,最多只能達到公尺級別。為了提高精確度,必須再採用相對定位(Relative Positioning)技術來輔助單點定位技術,相對定位技術可以將精確度提高至公分等級。在操作原理上,兩者並不相同。「單點定位」使用測距碼(Ranging Code)來測量虛擬距離(Code Pseudorange);「相對定位」則使用差分的(Differencing)載波相位測距(Carrier Phase Ranging)。
 圖1 GPS單點定位
圖1 GPS單點定位
 圖2 地球大氣層對GPS衛星通訊的干擾
圖2 地球大氣層對GPS衛星通訊的干擾
本文首先介紹屬於相對定位的GPS即時動態定位(Real Time Kinematic, RTK)技術,最後介紹手機結合了RTK接收模組和3D相機,能即時動態地拍攝出附高精確度參數值的3D點雲(Point Cloud)圖。
差分測距
「差分」可用來解決載波相位測距的週期模糊(Cycle Ambiguity)或載波相位模糊(Carrier Phase Ambiguity)問題。當GPS接收器的解調頻率和GPS衛星的載波頻率一樣,也就是鎖頻(Frequency-locking)時,接收器開始累計電磁波的週期數,該值乘以載波頻率的波長就是從鎖頻時的位置到接收器之間的距離。但接收器無法得知鎖頻之前電磁波週期的累加數量。使用差分測距可以算出這個值,亦即從GPS衛星到接收器鎖頻時的位置之間的距離。
常用的差分有三種:一次差分(Single Difference)、二次差分(Double Difference)、三次差分(Triple Difference)。一次差分又稱作接收器之間的差分(Between-receivers Difference),是一台使用了載波相位的GSP衛星同時由兩台接收器來測距。由於是同時測量,GPS衛星的時脈誤差可以被刪除。這從公式(1)到(4)中,可以清楚看出來。其中,

是k接收器測量到的虛擬距離,

是m接收器測量到的虛擬距離,k、m兩者的差就是

但在一次差分的情況下,k、m兩接收器之間的時脈誤差Tkm和正整數的週期模糊仍是未知數。在二次差分的情況下,如公式(5)和圖3,GPS衛星的時脈誤差Tp和k、m兩接收器之間的時脈誤差Tkm都被刪除了。k、m兩接收器之間的距離稱為基線(Baseline),當此基線很小時,因為對流層和電離層所產生的延遲皆可刪除不計。不過,使用二次差分測距仍無法消除週期模糊。圖4和圖5分別是一次差分測距和二次差分測距的立體示意圖,在這兩圖下方的數學式所代表的意義和公式(1)到(5)相同,只是使用的符號不同。

P代表接收器測量得出的虛擬距離(Pseudorange)。
k,m代表各接收器天線的相位中心點。
p,q代表GPS衛星發射源。
R代表GPS衛星到接收器之間的實際距離。
Q代表全部的雜訊(包含接收端的雜訊、多路徑造成的雜訊等)。
T代表GPS衛星或接收器的時脈誤差。
δtropo代表對流層引起的群波延遲(Group Delay)。
γiono代表電離層引起的延遲。
 圖3 二次差分測距的向量表示
圖3 二次差分測距的向量表示
 圖4 一次差分測距
圖4 一次差分測距
 圖5 二次差分測距
圖5 二次差分測距
三次差分測距主要是用來解決週期模糊問題。一旦解決了這個問題,就可以使用載波相位測距法,求出實際載波相位的總週波數和GPS衛星到接收器之間的實際距離,如公式(6)所示。圖6為三次差分測距的立體示意圖,兩台接收器在第一個時間點(epoch t1),同時測量GPS衛星a和b,接著在第二個時間點(epoch t2),兩台接收器再次同時測量GPS衛星a和b。t1和t2必須是一前一後的連續時間。如此,週期模糊可以被量化,在t1和t2的連續時間內,週期模糊應該是固定值。初始的週波數α不會變,為分數。兩台GPS衛星在t1到t2的連續時間內飛行,兩台接收器在初始時間過去後立即累計週波數β,為一直增加的整數。N是週期模糊,代表接收器在鎖頻時間點之前,GPS衛星和接收器之間的週波數或距離,如圖7。理論上,N應該也是固定值,除非因為失鎖(Loss-of-lock),造成週波脫落(Cycle Slip)。因此,在公式(6)中,理論上,只有β是未知的變數。在RTK的兩台接收站中,其中一台稱為參考站(Reference Station),GPS衛星預先得知其座標位置,假設此參考站所累計的載波相位總週波數為ϕk。另一台接收站因為一直在移動,稱為行動台(Rover),其所累計的總週波數假設為ϕm。將兩台累計的總週波數相減得出ϕk-ϕm=∆β。由於參考站到GPS衛星的實際距離Rk最快被算出來,行動台到GPS衛星的實際距離可由下列公式得出:Rm=Rk-λ∙∆β。當GPS衛星持續飛行、行動台持續移動時,Rk和Rm也隨著時間動態即時變化。實際上,參考站會不斷傳送即時的修正資訊給行動台,如此一來,行動台能夠得到高精確度的測距數據。

R是GPS衛星到接收器之間的實際距離。
λ是波長。
ϕ是載波相位的總週波數。
α是初始時的週波數(分數) 。
β是測量得出的週波數。
N是週期模糊。
 圖6 三次差分測距
圖6 三次差分測距
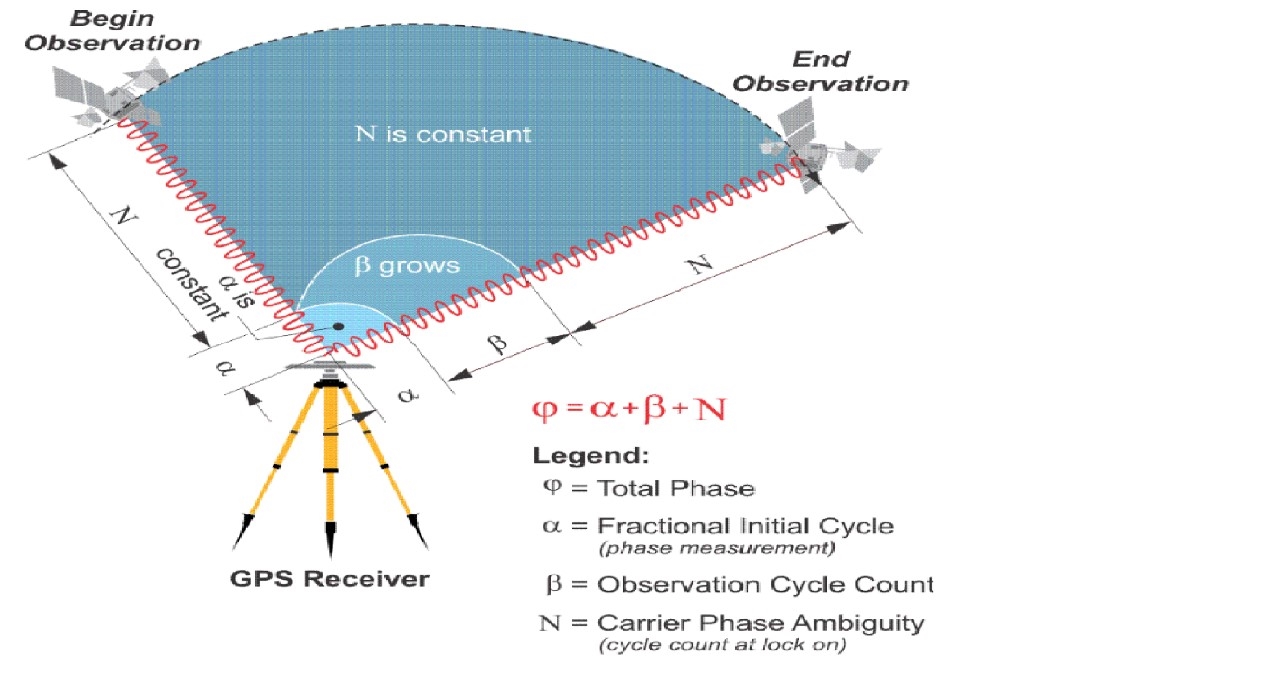 圖7 求解正整數的週期模糊
圖7 求解正整數的週期模糊
GPS即時動態定位技術介紹 差分測距實現公分級定位(1)
GPS即時動態定位技術介紹 差分測距實現公分級定位(2)